每日总结

每日总结

2022-7-18

今天，学长zh_dou为我们准备了四个非常简单的数论题，结果整寄了 😑

呜呜呜~ 😭

T1是一道莫反/容斥，都掌握的不太好，主要还是学到了Dirichlet 前缀和:

对于已知一个序列 $a$ ，求 一个序列 $b$ ：

$$b_k = \sum_{i | k} a_i$$

可以在$O(n\log\log n)$的时间复杂度内求出：

for(int i=1;i<=cnt;i++)
        for(int j=1;j*prime[i]<=n;j++)
            b[prime[i]*j]+=b[j];

T2拓欧+构造，很有意思

T3神一般的容斥

T4纯数学题，非常考验数学技巧。

开始搞数学了🙃

2022-7-19

数论！

2022-7-20

数论！！

2022-7-21

数论！！！

2022-9-4

算是做的一点题吧。

Test 1

T1 Not Equal Rectangle

玄学构造即可，首先考虑$n,m$非常小的情况，不难发现构造一个每条对角线上数字相同的矩阵就可满足，对于$n > 25, m > 25$时，可以考虑将整个矩阵划分为若干个上述$25 \times 25$的矩阵，然后将不同子矩阵上填的的数错开，即可，模数为23即可，数学证明略。

T2 One to One

可以发现，建好的边把点划分为若干个基环树和树。

• 如果为基环树，直接计算贡献为$a \times n^b$

• 如果是树，设$f_{i,j}$，转移方程为

  $$f_{i,j} = f_{i-1,j} + f_{i-1,j-1} \times size_i$$

  如果有$k$棵树，答案即为

  $$\sum_{i = 1} ^ k f_{k,i} \times (i-1)! \times n^{k-i}$$

T3 CF1109F Sasha and Algorithm of Silence’s Sounds

LCT + Segment tree 直接维护即可。

Test 2

T1 ARC134E Modulo Nim

首先可以看出0对结果无影响，以及相同的数对结果也没有影响，接下来考虑胜利条件，

当集合中有数$\le 2$时，很明显，{1}, {2},先手必败， {1，2} 先手必胜。

所有数$>2$时如果有奇数，则选择$m = 2$，剩余集合{1}, 先手必胜。

所有数都是偶数且有$\bmod 4 = 2$时，选择$m = 4$，剩余集合{2}，先手必胜。

考虑$m = 3$时，若剩余集合为{1}或{2},先手必胜。

若剩余几个为{1,2}，且所有数都是4的倍数，则剩余数只能形如$12k+4, 12k+8$，若此时集合为{4，8}. 先手必败，否则选择$m = 12$，先手必胜。

若剩余集合为{0}，所有数必须形如$12k$， 此时胜败不确定。

接下来分情况转移，状压转移胜负，最后用所有情况减去必败情况即为答案。

T2 ARC134F Flipping Coins

多项式 + 生成函数。

T3 CF1455G Forbidden Value

首先将指令看成树形结构，然后使用树形dp和启发式合并。

Test 3

T1 二龙戏珠

典型的卡特兰数例题，其实就是求从(0,0)走到(n,m) 且不经过直线$y = Ax +B$上方的方案数。

答案即为

$$C_{n+m} ^ n - A \times C_{n+m} ^ {n-1}$$

T2 老鼠偷奶酪

模拟。

T3 脑袋砸核桃

问题可以转化为gcd卷积，即求$\sum_{\gcd(i,j) = x} a_i b_j$，使用后缀和和后缀差分实现。

T4 巨斧砍大树

LCT 动态维护最小生成树。

Test 4

T1 ARC124E Pass to Next

如果每个人都至少给出了一个球，其实可以让每个人都少给相同的个数，效果相同，所以至少有一个人没给球。

然后根据结论列出dp方程即可。

T2 CF1470E Strange Permutation

由于操作互不重叠，可以将原问题转化为求翻转操作，二分 + 递推即可。

T3 P8434 「WHOI-2」D&D

集合 $A$的装饰子集即不被其它任何数包含的子集，$a$ 包含 $b$ 当且仅当 $a | b = a$，即 $b$ 为 1 的位 $a$ 也为 1。

考虑原序列的装饰子集 $S$，假设 $x\in S$，因为 $x$ 不被任何数包含，所以对于任意子串 $[l,r], x$ 同样不被区间内任何数包含。因此 $x$必然作为某个划分子串的装饰子集内的一个元素。所有子串的装饰子集包含 $S$。

考虑 $x\notin S$，假设存在 $y\in a_i$ 包含 $x$。因 $x$不可能作为 $y$ 所在子串的装饰子集，故所有子串的装饰子集不包含 $S$ 以外的元素。

这证明了所有子串装饰子集等于 $S$。

令 $l_i$ 表示使得 $[l_i, i]$包含所有 $S$内元素的最大的 $l_i$,显然可以双指针求出。

容易得到 DP $f_i$ 表示 $[1, i]$的答案，$f_1 = 0$.若 $l_i$ 存在，则有转移方程 $f_i = \sum\limits_{j = 0} ^ {l_i - 1} f_j$，表示将$[j, i](j \le l_i)$ 划为子串。前缀和优化即可做到 $\mathcal{O}(n)$。

求 $S$ 相当容易，只需对每个数 $a_i$ 检查是否存在$a_j\neq a_i$有 $a_j$包含 $a_i$,可以再搞个 DP 算这玩意，也可以直接高维后缀和，相当好写。

Test 5

T1 robo

模拟。

T2 expand

先预处理出最短路和最大体积然后状压dp转移即可。

T3 birthday

根据抽屉原理对于操作1当区间长度大于13时肯定会得到yes，所以当区间长度小于14时二分搜索即可，对于操作2线段树维护即可，到叶子节点时在下穿tag。

Test 6

T1 trees

考虑每个权值的影响，将权值从小到大排序后，即可得到答案为：

$$\sum_{i = 1}^n val[i] \times C_{i-1}^{k-1}$$

T2 bridge

矩阵加速递推。

T3 flowers

寻找循环节即可。

2022-9-10

小总结（

Test 1

T1 ARC100E Or Plus Max

考虑枚举子集，维护每个集合的最大值和次大值，最后统一取$max$即可。

T2 CF615F LEGOndary Grandmaster

可以对题意使用技巧, 将原来的$01$串的偶数维取反，每次在原串的取反操作等价于在新串中交换两个相邻的字符，然后就可以巧妙的将问题转化为：交换新串的字符，将其变为目标串。

很显然，首先两个串的$1$的个数要相同，然后不难得出，设$s$中第$i$个$1$的下标为$x_i$，$t$中第$i$个$1$的下表为$y_i$，最少交换次数就为$\sum_{i = 1}^n | x_i - y_i|$，$n$为其中$1$的个数，但是我们显然需要更好操作的形式，设$a_i$表示$s$中前$i$个数中$1$的个数， $b_i$表示$t$中前$i$个数中$1$的个数，答案就变为了$\sum_{i = 1} ^ n |a_i - b_i|$，然后直接统计前缀， 后缀中等于$a_i - b_i = j$的个数$\times j$就好了。

时间复杂度$O(n^2)$。

T3 数列

显然对于没一个位置的答案就是$suf _ {max}-pre_{min}$，直接统计删去每个数的贡献就可以了。

Test 2

T1 排列

如果不加任何限制，显然将所有的正数排列在一起是最优的答案，也就是说当有必须的限制，让一个负数夹在两个证数之间时，会对答案产生影响，这时会有三个选择，要么选择前面的答案，要么算上负数，要么选择后面的答案， 不难想到，可以用最小割来解决这个问题。

将每个位置拆成两个点$l, r$，如果当前位置是一个正数，将$s$连向$l$， $r$ 连向$t$，权值为正数的值，统计和，如果是一个负数，就将$l$连向$r$， 权值为其绝对值，对于每一个限制$(a, b)$， 将$l_a$连向$l_b$， $r_a$连向$r_b$就好了， 跑最小割来得到答案。

T2 ARC127F ±AB

结论题， 类似欧几里得算法。

T3 CF1616H Keep XOR Low

建$01$trie, 设$f(u, v)$表示从$u$的子树和$v$的子树中选一些数，两两异或不大于$x$的方案数， 类似树形dp转移即可。

Test 3

T1 珠江夜游

画一次函数图像就可以很直观的看出答案一定是最靠右的与$dist$的交点， $O(n)$即可解决。

T2 旅行计划

欧拉路径

T3 基站建设

二维区间dp， 转移即可。

Test 4

T1 ARC101E Ribbons on Tree

巧妙的树形dp， 用了一手容斥的技巧。

T2 ARC088E Papple Sort

很明显的贪心思路就是对于每一种字符，位置靠右的肯定要对上位置靠左的来让移动步数最少， 这样我们就可以先对每一个字符标上编号， 问题就转化成了统计逆序对个数。

T3 交换

分治维护一个栈，同时统计方案数。

Test 5

T1 CF1422F Boring Queries

首先对于每个大于$\sqrt {2e5}$的大质数显然只会出现了一次， 小于$\sqrt{2e5}$的质数有$86$个， 这样就可以对于小的质数用RMQ求解，大质数就可以统计$[l,r]$内不同数的个数来计算贡献，主席树维护。

T2 序列

不错的期望dp

T3 CF741D Arpa’s letter-marked tree and Mehrdad’s Dokhtar-kosh paths

上古神题了，算是dsu的应用好题，（毕竟是算法提出者本人出的题）。

由于只需要统计$a - v$这$22$个字母，可以考虑用二进制压缩，对于能以构成回文路径的肯定是只有一个字符出现了奇数次或均出现了偶数次，可以二进制压缩表示每个字符的奇偶性状态，然后根据异或的性质，维护根到当前节点的异或值，$dis_x \oplus dis_y$， 就可以得到$x$到$y$的路径的状态。

首先合法的状态只有$23$种，直接可以开桶跑dsu on tree，暴力枚举状态就可以解决了。

2022-9-14

Test 1

T1 树

首先考虑莫比乌斯反演，变为统计 $k∣gcd$ 的点对数量。 对于每个边权，首先去掉重复的质因子，这样它的质因子只有不超过 $c=7$个。 那么对于每个 $k$，将边权是 $k$ 的倍数的边取出，用并查集计算答案。 对于修改涉及的边，我们一开始不将它们加入并查集。然后我们枚举 $q+1$ 个时刻，再将这些边加入，统计答案，再删去即可。 时间复杂度 $O(L+(n+q^2)2^c\log n)$。

T2 ARC133D Range XOR

把它们模4的结果进行分类，我们可以得到:

$$w_{4x}=x \\ w_{4x+1}=1\\ w_{4x+2}=x+1\\ w_{4x+3}=0\\$$

可以用数位dp解决，$f[i][j][k]$表示还有 $i$ 位,第一个数是否卡上界，第二个数是否卡上界的方案数。

T3 CF1503E 2-Coloring

合法的情形其实就是以下情况：

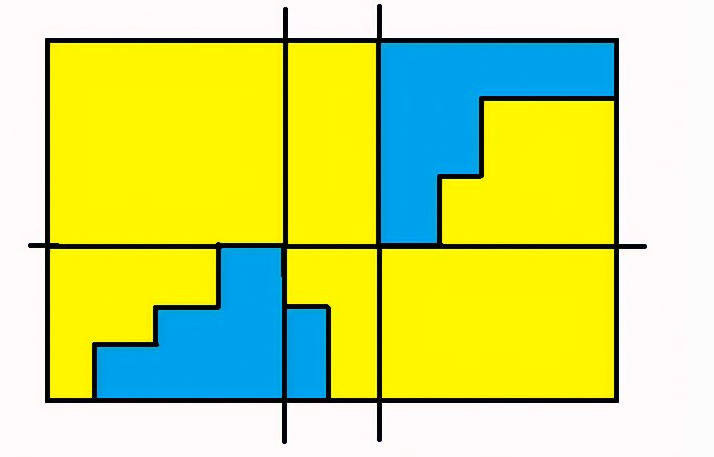
然后将直接统计即可。

Test 2

T1 tree

在$A$树上建主席树， 每个点上储存到根路径上的信息。求出每个点在$B$树上的DFS序，然变后成一个区间最大值的问题，这样就处理好了每个$A$树上的点在$B$树的贡献。

T2 ARC111E Simple Math 3

考虑$i$的取值， 可以得到$i \le \lfloor \frac{d- 2}{c - b} \rfloor$，设$m = \lfloor \frac{d- 2}{c - b} \rfloor$然后答案就为：

$$m - \sum_{i = 1} ^ {m} (\lfloor \frac{a + ci}{d} \rfloor - \lfloor \frac{a - 1+ bi}{d} \rfloor)$$

类欧几里得解决即可。

T3 ARC101F Robots and Exits

将操作映射到平面直角坐标系上就不难得出状态转移方程， 树状数组优化一下就好了。

2022-9-24

Test 1

T1 note

其实对于一定满足题意的$N$最大可以为$102345678900000$，其实求解数列$A$满足$A_i = A_{i - 1} + 1$，并且构成$A_i$的数字中必须包换数列$B$，也就是说我们可以先枚举数列$A$，直接暴力去求$\lfloor \frac{A}{10} \rfloor$，去判断满足了那些$B_i$ 然后去除这一位去构造新的数列$A'$这样做的话每次数列长度会变为原先的$\frac{1}{10}$，复杂度$O(\lg n)$。

T2 CF1119H Triple

首先题目要求的其实就是$n$个桶$xor$卷积后的结果，不难写出一个$O(n2^k)$的转移dp，但其实可以转化为多项式的形式，用FWT解决， 首先构造多项式为：

$$F_{i, j} = (-1) ^ {g(j \& a_i)}x + (-1)^{g(j \& b_i)}y + (-1) ^ {g(j \& c_i)}z$$

然后考虑化简式子：

$$\prod F_{i, j} = \prod \bigg( (-1) ^ {g(j \& a_i)}x + (-1)^{g(j \& b_i)}y + (-1) ^ {g(j \& c_i)}z \bigg)$$

将其都异或上$a_i$，然后就可以设出方程

$$c_1 + c_2 - c_3 - c_4 = \sum_i F_{i, j}$$

问题就可以得到解决了

T3 CF241B Friends

主要是用到了01trie 上二分的方式求出第k大， 然后将每一位拆开， 一位一位的加就可以用$O(n \log n)$的复杂度解决这个问题了

Test 2

T1 axelavir

打表题， 有OIES做法，也可以使用dp转移

T2 ARC111F Do you like query problems?

首先可以将和去转换成期望， 最后答案乘上方案数， 每次操作对答案的影响其实就是

$$\frac{1}{2 m + 1} E(\sum_{i = l} ^ r a_{i, j})$$

求的就是对应的$q$次求和，由于期望是线性的可以对每个$a_i$单独计算贡献，

$$\begin{aligned} \sum_{j = 1} ^ q \frac{1}{2 m + 1} E(\sum_{i = l} ^ r a_{i, j}) & = \sum_{j = 1} ^ q \frac{1}{2 m + 1} \sum_{i = 1} ^ n \frac{i (n - i + 1)}{\frac{n (n + 1)}{2}} E(a_{i, j}) \end{aligned}$$

然后化简式子即可得到答案为

$$\frac{m - 1} { n(n + 1)(2 m + 1)} \sum_{i = 1} ^ n i(n - i + 1)\sum_{j = 1} ^ q (1 - (1 - P_i)^ {j - 1})$$

T3 ARC120E 1D Party

首先对于每个点的运动过程可以画成图像：

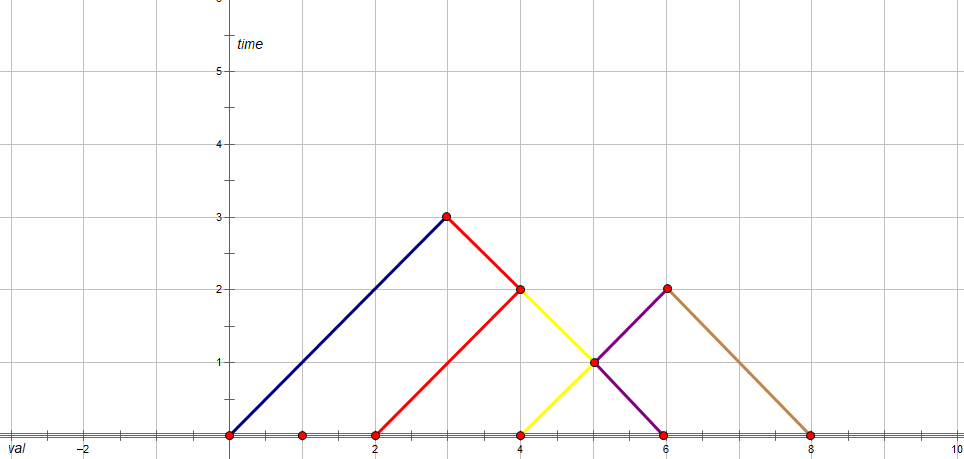
不同颜色代表不同的路径其实对应的答案就是最高点，然后将其转化为若干个三角形

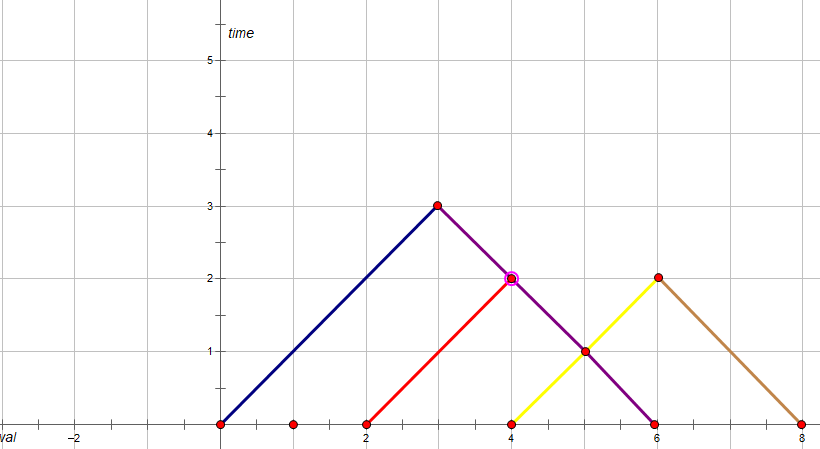
然后就可以得到一个$O(n ^ 2)$的转移方程：

$$f_i= \min_{j= 1} ^ {i - 2} (\max(f_j, \frac{a_i - a_{j - 1}}{2}))$$

考虑优化转移，其实上述方程枚举了许多无用状态，手玩可知， 只需要从有$4$个点的三角形和$5$个点的三角形转移过来就行了， 更多的点的三角形其实可以拆成$4$个点和$5$个点的。

然后方程就转化为了

$$f_i = \min(\max(f_{i - 2}, \frac{a_i - a_{i - 3}}{2}),\max(f_{i -3}, \frac{a_i - a_{i -4}}{2}))$$

时间复杂度$O(n)$。

Test 3

T1 导出子图

状压dp即可

T2 ARC135 F Delete 1, 4, 7, …

设$f(i) =\lfloor \frac{3i + 1}{2} \rfloor$， 那么$f(i)$其实就是第一次操作后第$i$个位置的数， 设第$k$次操作后位置$i$为$f^k(i)$， 然后有

$$f^k(n + 2 ^ k) = f^k n + 3 ^ k$$

数学归纳法可证，然后预处理进行二进制拆分即可做到$O(2^y \log n + 2^x k)$的时间复杂度。

T3 ARC 138 D Priority Queue

首先把所有可能的最终集合排序并找到字典序， 最大的，显然就是贪心的子啊第$i$次插入时插入$i$即可，然后就可以设出一个$O(n ^ 2)$的dp,状压一下即可。

Test 4

T1 归并

其实根据题意不难发现，比较时对于这两段区间的最大值是递增的， 插入的区间是连续的，可以建一棵平衡树，修改时比较两段的当前最大值即可，时间复杂度是均摊的可以通过此题。

T2 ARC112E Cigar Box

首先考虑每一次操作只有最后一次操作才是有意义的，首先考虑一个长度为$k$的操作序列， 对答案的贡献就是$\dbinom{m}{k}$，再加上放的方向为$\dbinom{m}{k} 2 ^ {m - k}$,再去考虑递增区间作为合法区间的影响， 答案即为

$$\sum _ {i = 0} f(i) \dbinom{m}{i} 2 ^ {m - i}$$

T3 ARC120F Wine Thief

定义$f(n, k)$为在一个长度为$n$的环内取$k$个的方案数，$g(n, k)$为在长度为$n$的数组内取$k$个数的方案数，不难得出$g(n, k) = \dbinom{n - k + 1}{k}$,$f(n, k) = g(n - 1, k) + g(n - 3, k - 1)$， 统计出现次数计算答案即可。

2022-9-27

Test 1

T1 牛堡的十字路口

斜率优化dp

T2 CF1109E Sasha and a Very Easy Test

其实就是用数据结构维护任意模数的区间乘，单点除， 区间求和，首先观察数据范围，每个数质因数分解后，质因数的个数不会超过$10$个在进行除的时候，由于题目中满足一定可以整除，取模时把数拆成与模数互质和不互质的部分，然后互质的部分， 之间求逆元， 不互质的部分就去对质因子进行减操作，线段树维护即可。

T3 ARC087F Squirrel Migration

首先考虑什么样的排列能够使权值最大。

考虑权值上界：

对于每一条边，如果把它切掉则树会分成$S_1$ 和 $S_2$ 两个联通块，不妨 设$|S_1|\le |S_2|$。

那么这一条边显然最多被经过 $2|S_1|$ 次。

此时，$\forall u\in S_1,p_u\in S_2$。

考虑将重心 $G$ 拉出来作为根。如果存在多个重心则随便选一个即可。

那么现在每一个 $S_1$ 一定是一棵子树。

容易发现，使得权值最大的等价条件为 $\forall (G,v),u\in subtree(v),p_u\notin subree(v)$。

有了这个结论，就容易使用容斥求答案了。

$f_i$ 表示钦定 $i$ 个点不满足条件，剩下点任意的方案数。

则 $Ans=\sum (-1)^if_i(n-i)!$

单独考虑每一个$(G,v)$ 的 $subtree(v)$，设其大小为 $x$。

容易得到这个子树中$f_i=\binom{x}{i}^2i!$。

最终的 $f$ 把所有的子树使用背包合并起来即可，复杂度 $O(n^2)$。

2022-9-30

Test 1

T1 会议选址

首先， 一个点在一条链上动的时候， $dis(u,i)$为一个凸函数，可以使用树分治加速， 三度化平衡时间复杂度。

T2 CF618G Combining Slimes

可以根据期望的线性性对每个数分别统计贡献，设每个格子使得$j$至少出现一次的概率为$c_{i, j}$，然后就可以得到转移为

$$c_{i,j} = c_{i-1, j - 1} \times c_{i, j - 1}$$

再设$C_{i,j}$表示使用$i$个各自恰好出现一次$j$的概率

$$C_{i, j} = c_{i,h} \times (1 - c_{i- 1, j})$$

最终的转移方程$f_{i,j}$即为

$$f_{i,j} = j + \frac{\sum_{k = 1} ^ {j - 1} f_{i - 1, k} \times C_{i -1, k}}{\sum _{k = 1} ^ {j - 1} C_{i - 1, k}}$$

只处理前50项即可，矩乘。

T3 CF1609G A Stroll Around the Matrix

由于$a, b$的差分数列均为单调递增的，可以证明每次选差分值小的走会最优，再考虑每个差分值的贡献， 贡献即为

$$\sum_{i = 1} ^ {n + m - 2} d_i \times (n + m -i - 1)$$

最后要加上$(a[1] + b[1]) \times(n + m - 1)$即为答案。

注意到$n \le 100$， 可以用线段树维护$b$， 暴力更改$a$，每次对差分值排序， 对于每个$a_i$在$b$的线段树上二分即可。

2022-10-3

Test 1

T1 P3616 富金森林公园

观察题目其实是在求对于每一个询问的高度$x$， 求满足$h _ {i - 1} < x \le h_i$的个数，线段树区间修改，单点查询即可。

T2 区间排序

如果排完序想要相同的话,那么 $max-min+1=r-l+1-x$（$x$是区间不是第一次出现的数) 化简得 $max-min+x+l=r$从坐往右扫,$max min$ 使用单调栈维护,$x$用个$map$记录上次出现位置,l是定值即可,复杂度$O(n \log n)$。

2022-10-5

Test 1

T1 小K的外挂

设$f_i$为向左走再向右跳的最大值，$g_i$为次大值， 每次跳的时候，如果遇到标记的就去跳次大值，否则跳最大值，倍增即可。

T2 小Z的作业

设$f_i$表示以$i$为左端点，能满足条件的右端点的最小值，不难发现$f_i$是单调递增的可以倒着加边，LCT维护去更新$f_i$，查询是$O(1)$的， 用LCT维护时开一个set来维护加入的能以让联通块减少的边，当加入边时如果两点已经联通，就去删去两点路径上的编号最大的边， 总体把边当成点建边即可。

2022-10-8

Test 1

T1 分组

考虑贪心将每一个字符串倒过来建一棵trie树，然后在树上贪心即可。

T2 ARC136E Non-coprime DAG

令$f(x)$为$x$的最小质因子，考虑$x$可以到达$y$的条件，按照奇偶性分类：

• $2 \mid x, 2 \mid y$， $x$肯定可以到达$y$
• $2 \not \mid x, 2 \mid y$， $x + f(x) \le y$
• $2 \mid x, 2 \not \mid y$，$2 \le y - f(y)$
• $2 \not \mid x, 2 \not \mid y$，$x + f(x) \le y - f(y)$

然后考虑对应的贡献区间为$[x - f(x) + 1，n + f(x) - 1]$，然后差分前缀和取$\max$即可。

T3 美好的每一天~不连续的存在

我的评价是听说gal挺好玩，建议去玩。

Test 2

T1 小D的序列

可以用等差数列求和公式判断。

T2 小S排座位

贪心前缀后缀即可。

Test 3

T1 sequence

主席树二分。

T2 训练(train)

区间dp。

T3 糖果(candy)

贪心，其实就像是一个二分图匹配， 先预处理出在每个点可以选的符合要求的点，然后再处理对应的点集， 选的时候，选点集大小小的，就像一个二分图匹配的过程。

T4 遗迹(ruin)

组合数学 + dp。

Test 3

T1 题目

折半搜索即可。

T2 名字

据期望线性性，询问的答案就是 $E(dep(u))+E(dep(v))−2×E(dep(lca(u,v)))$。

$E(dep(u))$很好求，直接枚举$u$ 的父亲是谁就行

设 $u<v$则 $E(dep(lca(u,v)))$只跟 $u$有关，证明即考虑 $v$ 一直向上跳，跳到第一个编号 $≤u$的点，那么这个点以正比于 $a$ 的概率在 $[1,u]$中随机。

如果跳到了 $u$，那么期望深度就是 $E(dep(u))$则设跳到的点是 $x(x<u)$期望深度就是 $E(dep(lca(x,u)))$，这只与$x$有关，用类似上面的方法递推就行。

时间复杂度 $O(nlogmod+q)$，可以离线求逆元做到 $O(n+logmod+q)$。

2022-10-17

Test 1

T1 CF311B Cats Transport

对于每一只猫可以计算出何时出发的人可以正好接走它。
如此得到一个长 $m$ 的时间数组 $t$，将它从小到大排序。
题意变为：把数组分为$p$段，每段的代价是所有数与该段最大值的差值之和。求最小代价。
令$S$ 数组为$t$数组的前缀和。 所求即为

$$f_{i, j} = \min_{k = 0} ^ {j - 1} \{ f_{i - 1, k} + t_j \times (j - k) - S_j + S_k \}$$

然后斜率优化即可。

T2 CF1553F Pairwise Modulo

首先先将答案拆成两部分计算，然后对于每一部分，考虑直接暴力枚举， 由于$a_i$互不相同，时间复杂度均摊下来是$n \log m$的，可以通过。

T3 CF1693D Decinc Dividing

首先观察题目不难得出一个结论那就是， 对于一个子区间$[l, r]$，有解的充要条件是，

不存在$l \le a < b < c < d \le r$， 使得$p_b > p_a > p_d > p_c$或$p_b < p_a < p_d < p_c$，然后直接用单调栈维护即可。

Test 2

T1 CF1396D Rainbow Rectangles

不妨反过来考虑，先处理出最终的答案，然后逆着处理，每次删除一个新颜色 $[pre_c,i]$的答案会取$\max$，然后每次查询一次全局贡献和。显然这是可以使用线段树维护的，然而直接取 $\max$,由于$f(l)$是单调的可以直接写一个线段树二分找到对应区间， 然后执行区间覆盖即可，时间复杂度$O(n^2 \log n)$。

T2 最长上升连续子序列

直接构造多项式求解。

T3 Die Siedler

考虑转化问题，将每个位置的卡牌转移到第一个位置上来，首先对于这种转化方式容易得到其得到满足要求的序列所需的最小步数，是与原序列是等价的，同时对于每种卡包， 也用相同的转化方式，然后相加减的答案就是原序列的答案。

对于一个长度为$n$的序列，其转化即为

$$\sum_{i = 1} ^n a_i 2 ^ {i - 1} (i - 1) !$$

然后考虑已知这种表达方式如何求解，其实只要贪心即可，去倒着填，对于第一个位置的数，其可以减少若干倍的$2 ^ n n! - 1$(转化一周)， 也就是说，最后所有卡牌转为为第一个位置的时候，答案可以表示为，

$$v = R + \sum_{i = 1} ^ n b_i x_i - y (2 ^ n n! - 1)$$

裴蜀定理解出即可， 然后考虑到数据范围，需要使用根号分治，当$d < \sqrt {2 ^ n n !}$时，直接暴力枚举，$d \le \sqrt {2 ^n n!}$时，根据转移，可以跑同余最短路，然后问题就解决了。

Test 3

T1 花环

哈希解决即可。

T2 最短最长最短路

可以根据竞赛图一个点到其他点的距离不超过$2$的性质，直接得出答案。

T3 花环

区间dp转移即可。

T4 二分图最大权匹配

根据曼哈顿距离的性质，直接建图即可。

Test 4

T1 sequence

$K$段求和的 $\gcd$ 等于$K$段右端点前缀和的 $\gcd$

也就是求最大的数 $x$ 使得 $x|sum_N$，且有 $K−1$ 个 $p$满足 $x|sum_p$

可以 $O(N+σ1V)$ 求出。

T2 xor

笛卡尔树分治过程中$0-1$ trie启发式合并即可。

T3 dawn

约瑟夫环上的nim游戏。

T4 nogirlfriend

后缀数组加平衡树维护。

Test 5

T1 brime

直接筛素数，枚举即可，复杂度$k \ln n$，$k$为质数个数。

T2 sequence

dp矩阵优化转移。

T3 iiidx

线段树维护期望值即可。

T4 inception

对于每次询问建虚树然后，大力分类讨论，即可。

2022-11-3

Test 1

T1 正方形

可以先将所有询问下来， 然后预处理出以每个点为右下角的最大边长，排序后，从大到小，依次加点用并查集维护连通性即可。

T2 计数

可以用范德蒙德卷积。

2022-11-10

Test 1

T1 GCD和LCM

求的柿子为，

$$\begin{aligned} \\ ans &= \sum_{i = 1} ^ n \sum_{j = 1} ^ m lcm(i,j) [\gcd(i,j) \le k]\\ & = \sum_{t = 1} ^k \sum_{i = 1} ^ n\sum_{j = 1} ^ m lcm(i, j) [\gcd(i, j) = t] \\ &= \sum_{t = 1} ^ k \sum_{i = 1} ^ n \sum_{j = 1} ^ m \frac{ij}{\gcd(i, j)}[\gcd(i, j) = t] \\ &= \sum_{t = 1} ^ k t \sum_{i = 1} ^ {\lfloor \frac{n}{t} \rfloor} \sum_{j = 1} ^ {\lfloor \frac{m}{t} \rfloor} ij [\gcd(i, j) = 1] \\ &= \sum_{t = 1} ^ k t \sum_{i = 1} ^ {\lfloor \frac{n}{t} \rfloor} \sum_{j = 1} ^ {\lfloor \frac{m}{t} \rfloor} ij \sum_{d | \gcd(i, j)} \mu(d) \\ &= \sum_{t = 1} ^ k t \sum_{d = 1} \mu(d) d^2 \sum_{i = 1} ^ {\lfloor \frac{n}{td} \rfloor}\sum_{j = 1} ^ {\lfloor \frac{m}{td} \rfloor} ij \\ \end{aligned} \\$$

观察数据范围，需要进一步优化，考虑枚举$td$，并将后面的求和设为$S(x)$，

$$ans = \sum_{p = 1} S(\lfloor \frac{n}{p} \rfloor) S(\lfloor \frac{m}{p} \rfloor) \sum_{1 \le d \le k, d|p} \frac{p^2}{d} \mu(\frac{p}{d}) \\$$

然后将数据离线下来，按照$k$排序后，每次移动上界用树状数组维护对于每个$p$下的$\sum_{1 \le d \le k, d|p} \frac{p^2}{d} \mu(\frac{p}{d})$，每个答案求和即可，时间复杂度$O(q\sqrt n \log n + n \log^2 n)$。

T2 平面图

直接平面图转对偶图，启发式分裂完事了。

2022-11-11

Test 1

T1 序列

直接跑DAG上的dp即可。

T2

直接猜结论，随便证一证就可以发现，可以先把树处理出来，对于非树边上的权值，进行树上路径的最小值覆盖即可。

T3

首先观察到质因子数会很少，直接状压DP即可。

T4

考虑化简柿子为，

$$\max\{ a_i, i \in [l, r] \} - \min\{ a_i, i \in [l, r] \} \le r - l + k$$

换一下柿子维护即可。