高数必备

数值积分

前置知识

我也不知道为什么突然来到了高等数学，那就胡一下吧，也许主要写的是高等数学？。

tips:以下内容仅供参考，毕竟是胡的

导数

导数(Derivative)，也称为导函数值，又名微商。在数学中发挥着很重要的作用。

导数是函数的局部性质。一个函数在某一点的导数描述了这个函数在这一点附近的变化率。如果函数的自变量和取值都是实数的话，函数在某一点的导数就是该函数所代表的曲线在这一点上的切线斜率。导数的本质是通过极限的概念对函数进行局部的线性逼近。 ——––baidu

其实通俗的来讲导数就是一个函数的变化率，比较经典的就是二次函数求切线。

假设我们要求某一光滑曲线在$M$点的切线，先在函数图像上取一点$N$，假设直线$MT$为$M$点的切线，当$\angle {NMT}$无限小时此时的直线$MN$就已经成为切线，设直线$MN$的斜率为$\tan \phi$，有：

$$\tan \phi = \frac{f(x) - f(x_0)}{x-x_0}$$

当$N$逼近与$M$时，

$$\tan \phi = \lim\limits_{x \to x_0} \frac{f(x) - f(x_0)}{x-x_0}$$

令$\Delta x = x-x_0$，所以

$$\tan \phi = \lim\limits_{x \to 0} \frac{f(x_0+\Delta x) - f(x_0)}{\Delta x}$$

此处 $\tan \phi$即为函数在$x_0$处导数的取值，现在引出导数真正的 emp 定义 。

假设函数$y = f(x)$在点$x_0$处的邻域有定义，当自变量$x$在$x_0$处取得增量$\Delta x$(仍然在邻域内)，相应的函数取得增量$\Delta y = f(x_0+\Delta x) - f(x_0)$，如果$\frac{\Delta y}{\Delta x}$在$\Delta x \to 0$时的极限存在，称为函数$y = f(x)$在$x_0$处可导，它的导数可以写成

$$f'(x_0) = \lim\limits_{x \to 0} \frac{f(x_0+\Delta x) - f(x_0)}{\Delta x}$$

$f'(x_0)$也可以记成$\frac{\mathrm{d}y}{\mathrm{d}x}$或者$\frac{\mathrm{d}f(x)}{\mathrm{d}x}$,另外函数在$x_0$处可导的充分必要条件是，函数在$x_0$处的左右两侧的导数都 必须存在，并且相等 。

另外有一些函数的导数都是比较特殊的，这里就不再涉及。

微分

首先思考一个简答的问题，一个正方形金属薄片边长为$x$，受温度变化影响边长增加了$\Delta x$，求其面积变化了多少。

设正方形面积为$A$ ,这样我们就得到了一个函数$A = x^2$，计算$\Delta A$为:

$$\Delta A = (x_0+ \Delta x)^2 - x_0^2 = 2x_0\Delta x + (\Delta x)^2$$

首先第一部分$2 x_0 \Delta x$为一个线性函数，第二部分中当$\Delta x \to 0$时，$(\Delta x)^2$是比$\Delta x$高阶的无穷小，即$(\Delta x)^2 =\omicron(\Delta x)$

好了增量$\Delta y$现在已经可以表示为：

$$\Delta y = A \Delta x + \omicron(\Delta x )$$

其中$A$是不依赖$\Delta x$的常数，并且$\Delta y$与$A\Delta x$的差为：

$$\Delta y - A\Delta x =\omicron(\Delta x)$$

是比$\Delta x$更高阶的无穷小，这样当$A \ne 0$，且$|\Delta x |$无穷小时，$\Delta y$就可以近似的表示为$\Delta y = A \Delta x$。

接下来给出定义 ，设函数$y = f(x)$在某区间内有定义，$x_0$及$x_0+ \Delta x$在这段区间内，如果函数的增量

$$\Delta y = f(x_0 + \Delta x) - f(x_0)$$

可以表示为

$$\Delta y = A \Delta x + \omicron(\Delta x)$$

其中$A$是不依赖于$\Delta x$常数，那么称函数$y = f(x)$在$x_0$处是可微的，而$A\Delta x$叫做函数$y = f(x)$在$x_0$处相当于自变量增量 $\Delta x$的 微分(Differential) 记作$dy$，即

$$\mathrm{d}y = A \Delta x$$

积分

积分(integral)是微积分学与数学分析的一个核心概念。通常分为定积分和不定积分两种。（主要区别就是定积分得到的结果是一个数，不定积分得到的是函数）

tips：不定积分是求导运算的逆运算。这一结论被称为微积分基本定理 (fundamental theorem of calculus)。

直观的说，对于一个给定的正实数值函数，在一个实数区间上的定积分可以理解为在坐标平面上，由曲线，直线以及轴围围成的 曲边梯形的面积值（一种确定的实数值）

如果一个函数的积分存在，并且有限，就说这个函数是可积的。一般来说，被积函数不一定只有一个变量，积分域也可以是不同维度的空间，甚至是没有直观几何意义的抽象空间。对于只有一个变量$x$的实值函数$f$在闭区间$[a,b]$上的积分记作：

$$\int _{a}^{b} f(x) \mathrm{d}x$$

其中的$\mathrm{d}x$就是积分变量。

黎曼积分(Riemann Integral)，就是所说的正常积分，定积分。其求积分值的核心思想就是通过无限逼近来确定这个积分值，需要注意的是，如果$f(x)$去负值，则对应的面积值也为负值。

对于一个闭区间$[a,b]$的分割$P$就是指在这一个区间中取一个有限的点列$a = x_0 < x_1 < x_2 < \cdots < x_n = b$每个子区间长度的最大值定义为$\lambda = \max(x_{i+1}-x_i)$。

定义取样分割为在进行分割$P$后在每一个子区间$[x_{i},x_{i+1}]$中取出一点$x_i \le t_i \le x_{i+1}$,其区间长度最大值仍用$\lambda$来表示。

对于一个在区间$[a,b]$有定义的实值函数$f$，$f$关于取样分割$x_0 \cdots x_n , t_0 \cdots t_{n-1}$的黎曼和表示为：

$$\sum_{i=0}^{n-1}f(t_i)(x_{i+1}-x_i)$$

上述式子中的每一项是子区间长度$x_{i+1}- x_i$与在$t_i$处的$f(t_i)$的乘积，其实直观的来说就是将一个曲线梯形分割成无限个小的图形将其面积相加。

看来需要一个更严格的定义，我们需要把$\lambda$趋近于0函数值才能更精确。

设$S$是函数$f$在闭区间$[a,b]$上的黎曼积分，当且仅当$\forall \epsilon > 0, \exists \delta > 0$，使得$\forall x_0 \cdots x_n , t_0 \cdots t_{n-1}$，只要它的子区间长度最大值$\lambda \le \delta$就有：

$$\bigg| \sum_{i = 0}^{n-1} f(t_i)(x_{i+1} -x_i)-S \bigg| < \epsilon$$

也就是说，对于一个函数$f$，如果在闭区间$[a,b]$上无论如何取样分割，只要它的子区间长度最大值足够小，函数$f$的黎曼和都会趋向一个确定的值，那么在闭区间$[a,b]$上的黎曼积分存在，并且定义为黎曼和的极限，这时候我们称函数$f$为黎曼可积的。

黎曼积分还有一个更有操作性的积分定义叫做达布积分，（自行了解吧）。

还有一个非常重要的定理， 若$F(x)$为$f(x)$的不定积分 ，则$f(x)$为$F(x)$的导数；反之亦然。

根据以上定理，我们有：

$$\int_a^b f(x) \mathrm{d}x = F(b)-F(a)$$

正文

终于进入到了主题。

数值积分，是用来求定积分的近似值。

这里我们只阐述一种数值积分的求法，使用$Simpson$公式。

Simpson公式

$Simpson$公式就是在积分区间$[a,b]$中去找三个点$a,b$和$m = (a+b)/2$，计算其原函数在此处的值，然后用抛物线来拟合原函数。

tips：幂函数的积分公式：

$$\int x^{\alpha} \mathrm{d}x = \frac{1}{\alpha+1}x^{\alpha+1}+C \quad (\text{C为常数项})$$

尝试推导一下公式🤔

设$f(x)$为原函数，$g(x) = Ax^2 + Bx +C$为拟合后的函数，有：

$$\begin{aligned} \int_a^bf(x)\mathrm{d}x &\approx \int_a^b Ax^2 + Bx +C \\ &= \frac{A}{3}(b^3 - a^3) + \frac{B}{2}(b^2 - a^2) + C(a-b) \\ &= \frac{(b-a)}{6}\bigg(2A(b^2+ab+a^2)+3B(b+a)+6C \bigg) \\ &= \frac{(b-a)}{6}(2Ab^2 + 2 Aab +2Aa^2+3Bb+3Ba+6C) \\ &= \frac{(b-a)}{6}\bigg(Aa^2 + Ba+C+Ab^2 + Bb +C +4(A(\frac{a+b}{2})^2 + B(\frac{a+b}{2})+C)\bigg) \\ &= \frac{(b-a)}{6}\bigg(f(a)+f(b)+4f(\frac{a+b}{2})\bigg) \end{aligned}$$

最终$Simpson$公式为：

$$\int_a^b f(x) \mathrm{d}x \approx \frac{(b-a)(f(a)+f(b)+4f(\frac{a+b}{2}))}{6}$$

double simpson(double l, double r)
{
    return (r - l)*(f(l) + f(r) + 4*f((l+r)/2))/6;
}

有一个结论：$Simpson$公式的误差为

$$-\frac{1}{90}(\frac{r-l}{2})^5f^{(4)}(\xi)$$

其中$\xi$为区间$[l,r]$中的某个值。

是不是还没说数值积分学这玩意干嘛，很明显是解决积分问题的，想想上面我们说的黎曼积分的定义，其精确度很明显是由区间分割决定的，如何区间分割呢？

自适应Simpson法

现在来解决精度问题，让其实现自动控制分割区间的大小。

$Simpson$公式是通过一个二次函数去拟合原函数的，也就是说我们当前分割的区间对应的函数值越接近一个二次函数图像，误差就越小。

也就是说我们在计算时需要判断当前区间是否接近一个二次函数，判断过程如下：

首先将当前段直接代入求积分，在将当前这一段分成两个区间，求这两段的积分，如果当前段的积分值和分割成两段之后的积分之和相差很小的话就可以直接计算了否则递归。

有一个结论：三点$Simpson$与分成两个子区间后两个子区间$Simpson$和差值是原来绝对误差的$\frac{1}{15}$（我不太会证）

double auto_simpson(double l, double r, double eps, double fx)
{
    double mid = (l+r)/2;
    double L = simpson(l, mid);
    double R = simpson(mid, r);
    if(fabs(L + R - fx) <= 15*eps)
        return L + R + (L + R - fx)/15;
    else
        return auto_simpson(l, mid, eps/2, L)+
            auto_simpson(mid, r, eps/2, R);
}

The first question

给定积分：

$$\int_L^R \frac{cx+d}{ax+b} \mathrm{d}x$$

保留至小数点后六位。

直接使用公式即可。

或者直接积出来，直接暴切

#include <bits/stdc++.h>
using namespace std;

double a, b, c, d;

double f(double x)
{
    return (c*x + d)/(a*x + b);
}

double simpson(double l, double r)
{
    return (r - l)*(f(l) + f(r) + 4*f((l+r)/2))/6;
}

double auto_simpson(double l, double r, double eps, double fx)
{
    double mid = (l+r)/2;
    double L = simpson(l, mid);
    double R = simpson(mid, r);
    if(fabs(L + R - fx) <= 15*eps)
        return L + R + (L + R - fx)/15;
    else
        return auto_simpson(l, mid, eps/2, L)+
            auto_simpson(mid, r, eps/2, R);
}
int main()
{
    double l, r;
    scanf("%lf%lf%lf%lf%lf%lf", &a, &b, &c, &d, &l, &r);
    printf("%.6lf", auto_simpson(l, r, 1e-6, simpson(l, r)));
    return 0;
}

The second question

给定积分：

$$\int_0^{\infty} x ^{\frac{a}{x}-x} \mathrm{d}x$$

保留小数点后5位，会出现积分发散的情况。

好像这个式子是一个不可积分函数，只能用$Simpson$，(也只会$Simpson$),但是下界是0，上界是$\infty$，需要找到式子的一些性质。

可以证明：

• $a < 0$时原积分发散

  $$\begin{aligned} &\because \frac{a}{x} - x = \frac{a-x^2}{x} \\ &\therefore a-x^2 < 0,x^{\frac{a-x^2}{x}} = \frac{1}{x^{\frac{x^2-a}{x}}}\\ &\because x \to 0 ,x^2 \to 0, \frac{1}{x} \to \infty \\ &\therefore 0 < x < 1,x^k \to 0,k \to \infty \\ &\therefore x\to 0,f(x)\to \infty \end{aligned}$$

• $a>0$时原积分收敛

  $$\begin{aligned} &\because x^{\frac{a-x^2}{x}} = \frac{1}{x^{\frac{x^2-a}{x}}} \\ &\therefore x \to \infty ,f(x)\to 0 \end{aligned}$$

因为在$a>0$的时候收敛所以右边界不用设太大，可以自己打表试一下。

特判$a<0$，在$[1e-8,20]$作为积分范围即可。

#include <bits/stdc++.h>
using namespace std;

double a;

double f(double x)
{
    return pow(x, a/x - x);
}

double simpson(double l, double r)
{
    return (r - l)*(f(l) + f(r)+ 4*f((l+r)/2))/6;
}

double auto_simpson(double l, double r, double eps, double fx)
{
    double mid = (l+r)/2;
    double L = simpson(l, mid);
    double R = simpson(mid, r);
    if(fabs(L+R-fx) <= 15*eps)
        return L + R + (L + R - fx)/15;
    else
        return auto_simpson(l, mid, eps/2, L) +
            auto_simpson(mid, r, eps/2, R);
}
int main()
{
    scanf("%lf", &a);
    double l = 1e-9;
    double r = 20;
    if(a < 0)
        printf("orz");
    else
        printf("%.5lf", auto_simpson(l, r, 1e-8, simpson(l, r)));
    return 0;
}

The third question

给定一个由圆台和圆锥构成的组合体，给定一个角度求求其在平面上的投影面积。

体现了自适应辛普森法的一个常见用途，用来求曲边图形的面积 。

先来考虑投影的形状，首先一个圆的投影肯定是一个大小相同的圆，圆锥的投影就是一个圆加上了一个点，一级这个点和圆的两条切线，圆台的投影就是两个圆加上它们的公切线。

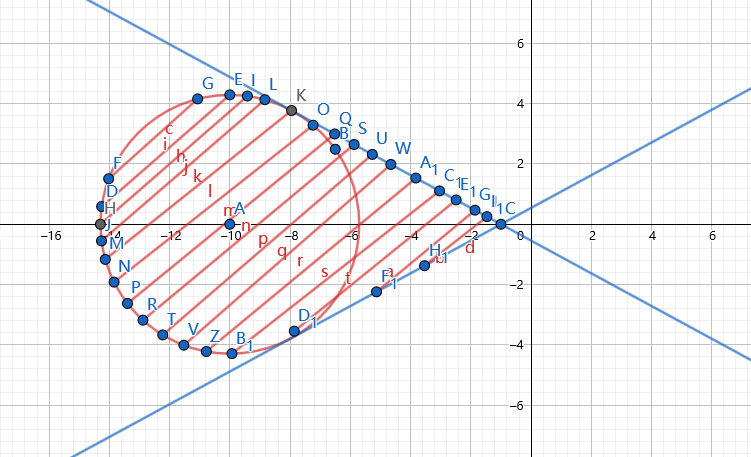
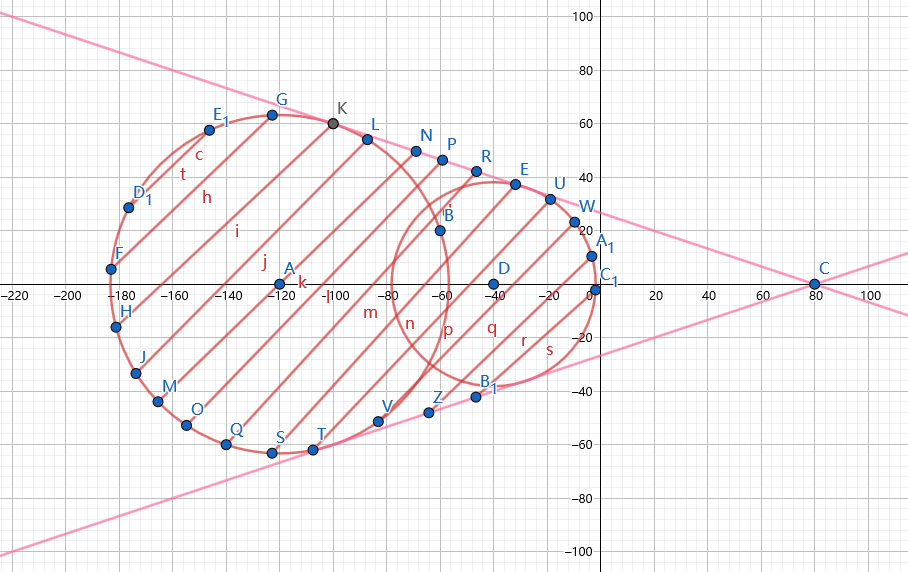
连起来的话就是一个非常鬼畜的东西。

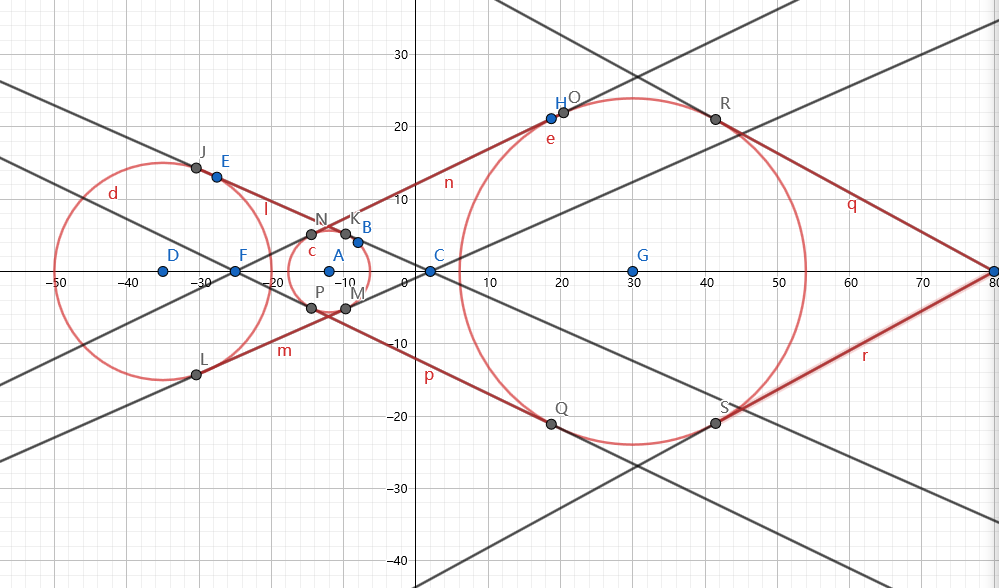
然后暴力即可（画的好像不太标准\kk）

是一个封闭图形，并且将其看作一个函数直接求积分即可。

再去观察图形，此时这棵树的投影已经变为了若干个圆弧加上若干个梯形和三角形。

既然是求积分的话而且还存在圆弧弧就需要用的$Simpson$公式了。

需要用梯形腰的左右两个端点作为一段函数的定义域。

然后就是高度为$h$的物体投影到水平面上长度会变为$\frac{h}{\tan \alpha}$，来确定横坐标。

#include <bits/stdc++.h>
#include <pthread.h>
#define dwd 1919810.114514
#define ochen 114514.1919810
using namespace std;

const int N = 510;

int n;
double alpha;
double H, Tan;

struct geometric{
    double x,y;
    geometric(double X=0,double Y=0):x(X),y(Y) {}
    friend geometric operator + (const geometric a,const geometric b){return geometric(a.x+b.x,a.y+b.y);} 
    friend geometric operator - (const geometric a,const geometric b){return geometric(a.x-b.x,a.y-b.y);} 
    friend geometric operator * (const geometric a,double p){return geometric(a.x*p,a.y*p);}
    friend geometric operator / (const geometric a,double p){return geometric(a.x/p,a.y/p);}// 向量的四则运算
    double dis(geometric a,geometric b){return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));} // 向量模长
    double dot(geometric a1,geometric a2,geometric b1,geometric b2){return (a2.x-a1.x)*(b2.x-b1.x)+(a2.y-a1.y)*(b2.y-b1.y);}// 点积
    double cross(geometric a1,geometric a2,geometric b1,geometric b2){return (a2.x-a1.x)*(b2.y-b1.y)-(a2.y-a1.y)*(b2.x-b1.x);} // 叉积
    double corner(geometric a1,geometric a2,geometric b1,geometric b2){return dot(a1,a2,b1,b2)/(dis(a1,a2)*dis(b1,b2));}// 向量夹角
    double area(geometric a1,geometric a2,geometric b1,geometric b2){return fabs(cross(a1,a2,b1,b2));}// 两向量围成的四边形面积
    double angle(geometric a){return atan2(a.y,a.x);}// 极角
    geometric rotate_counterclockwise(geometric a,double theta){return geometric(a.x*cos(theta)-a.y*sin(theta),a.x*sin(theta)+a.y*cos(theta));} // 向量逆时针旋转
    geometric rotate_clockwise(geometric a,double theta){return geometric(a.x*cos(theta)+a.y*sin(theta),-a.x*sin(theta)+a.y*cos(theta));} // 向量顺时针旋转
}opt;

struct circle{
    geometric p;
    double r;
    circle(geometric _p = 0, double _r = 0): p(_p), r(_r) {}
};
circle c[N];

struct line{
    geometric a, b;
    line(geometric _a = 0, geometric _b = 0):a(_a), b(_b) {}
    double calc(double x)
    {
        double k = (b.y-a.y)/(b.x-a.x);
        double b = a.y-k*a.x;
        return k*x+b;
    }
}seg[N];

double f(double x)
{
    double sum = 0;
    for(int i = 1; i <= n; i++)
    {
        if(x < c[i].p.x + c[i].r && x > c[i].p.x - c[i].r)
            sum = max(sum, sqrt(c[i].r*c[i].r-(x-c[i].p.x)*(x-c[i].p.x)));
    }//在圆里面
    for(int i = 1; i < n; i++)
    {
        if(x > seg[i].a.x && x < seg[i].b.x)
            sum = max(sum, seg[i].calc(x));
    }//在切线范围内
    //取最大可以满足所有情况
    return sum;
}

double simpson(double l, double r)
{
    return (r-l)*(f(l) + f(r) + 4*f((l+r)/2))/6;
}

double auto_simpson(double l, double r, double eps, double fx)
{
    double mid = (l+r)/2;
    double L = simpson(l, mid);
    double R = simpson(mid, r);
    if(fabs(L + R - fx) <= 15*eps)
        return L + R + (L + R - fx)/15;
    else
        return auto_simpson(l, mid, eps/2, L) + auto_simpson(mid, r, eps/2, R);
}

int main()
{
    scanf("%d%lf", &n, &alpha);
    Tan = 1.0/tan(alpha);
    n = n + 1;
    for(int i = 1; i <= n; i++)
    {
        double h;
        scanf("%lf", &h);
        c[i].p.x = h*Tan;
        c[i].p.x += c[i-1].p.x;
    }
    for(int i = 1; i < n; i++)
    {
        double r;
        scanf("%lf", &r);
        c[i].r = r;
    }// 输入
    c[n].r = 0;
    for(int i = 1; i < n; i++)
    {
        double x1 = c[i].p.x;
        double x2 = c[i+1].p.x;
        double r1 = c[i].r;
        double r2 = c[i+1].r;
        double a1 = r1*(r1-r2)/(x2-x1);
        double a2 = r2*(r1-r2)/(x2-x1);
        seg[i] = line(geometric(x1+a1, sqrt(r1*r1-a1*a1)),geometric(x2+a2, sqrt(r2*r2-a2*a2)));
    }//计算线段
    double l = c[1].p.x - c[1].r;
    double r = c[n].p.x - c[n].r;
    for(int i = 1; i <= n; i++)
    {
        l = min(l, c[i].p.x - c[i].r);
        r = max(r, c[i].p.x + c[i].r);
    }//必须计算积分区间。
    printf("%.2lf", 2*auto_simpson(l, r, 1e-6, simpson(l, r)));
    // 一遍只计算了一半
    return 0;
}

后记

其实高数挺多公式的，我这里就算随便提了一下吧。

参考文献

[1] 高等数学 同济大学数学系

[2]OIwiki-数值积分

[3]百度百科