反演变换
用的好像很少,毕竟是数竞知识。
反演变换
前言
反演变换适用于题目中出现多个圆或直线之间的相切关系的情况,反演变换可以有效简便的解决这类问题。
定义
设在平面内给定一点和常数,对于平面内任意一,确定,使为直线上一点,并且,我们称这种变换为反演变换,点即为反演中心为关于点的反演点。
反演变换本质上是属于平移,旋转,反射一类的几何变换。
以点为圆心,为半径作圆,就得到了一个圆的反演变换:
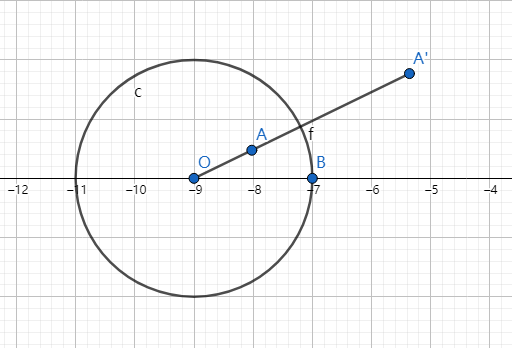
接下来讨论其相关性质。
性质
性质1
反演变换可逆
对于定义里的描述,为关于点的反演点,同时就有是关于的反演点。
性质2
- 在圆内的点其反演点一点在圆外
- 在圆外的点其反演点一定在圆内
- 在圆上的点的反演点与其在同一个位置
观察图形很容易得到的性质。
接下来引入一些几何图形关于圆的反演。
性质3
-
过反演中心的直线其反演后为自身
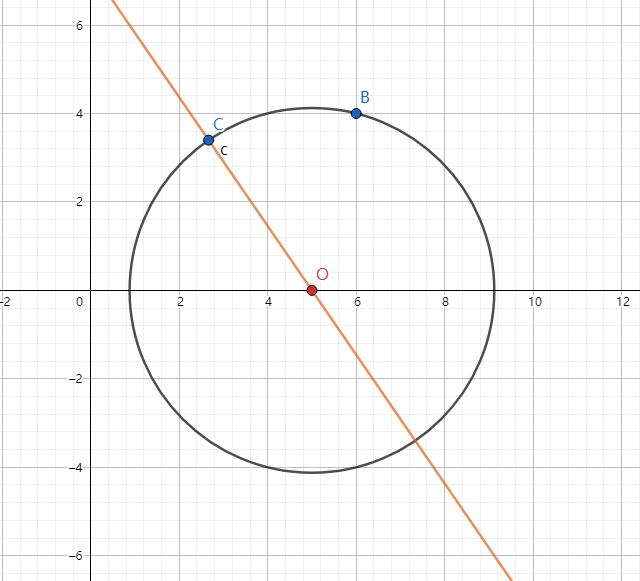
- 不过反演中心的直线,反演后为过反演中心的圆
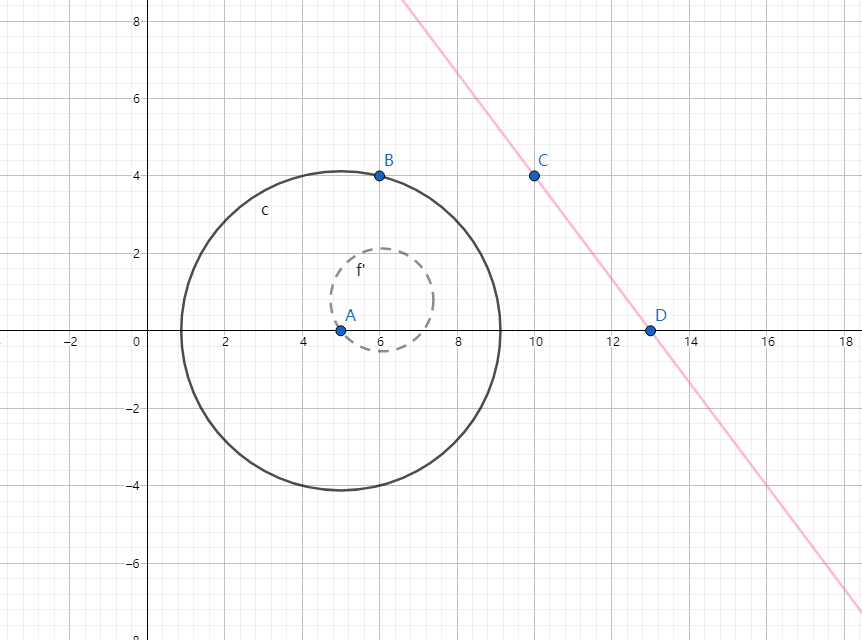
也许需要证明?也挺好推的,设反演中心为原点,直线解析式为,反演得到的线段为,可以推得交点为,设为,再设交点的反演点为,再根据反演的定义得,拆开后去掉常数项,会得到一个的圆的方程。
性质4
-
不过反演中心的圆,其反演后仍为一个不过反演中心的圆
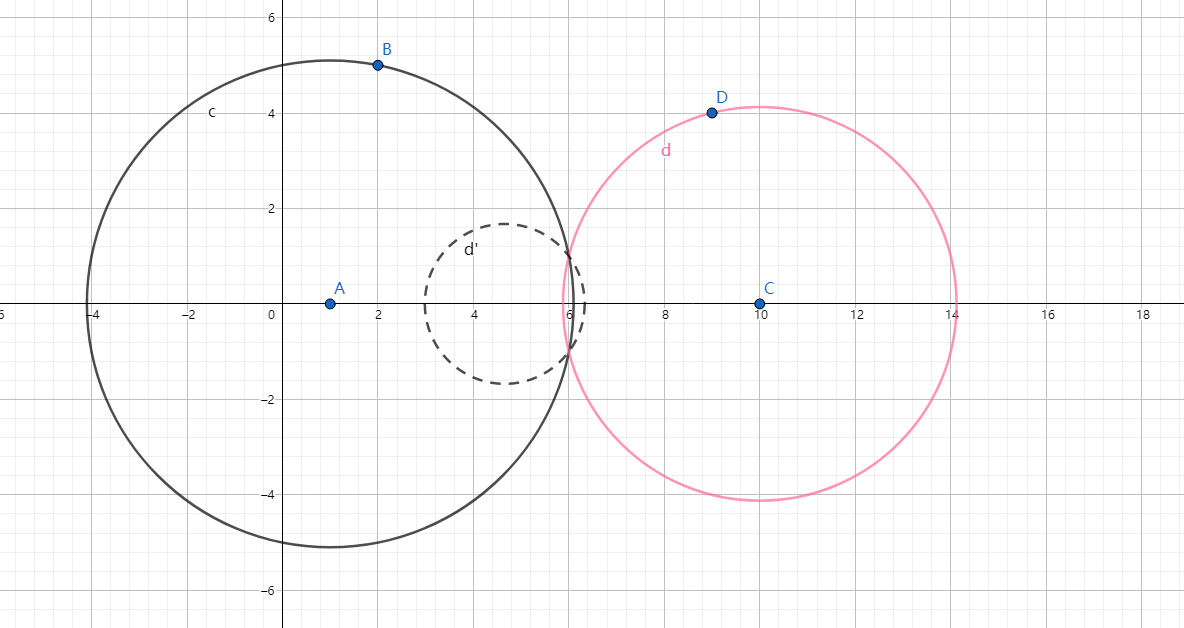
-
过反演中心的圆,其反演后为不过反演中心的一条直线
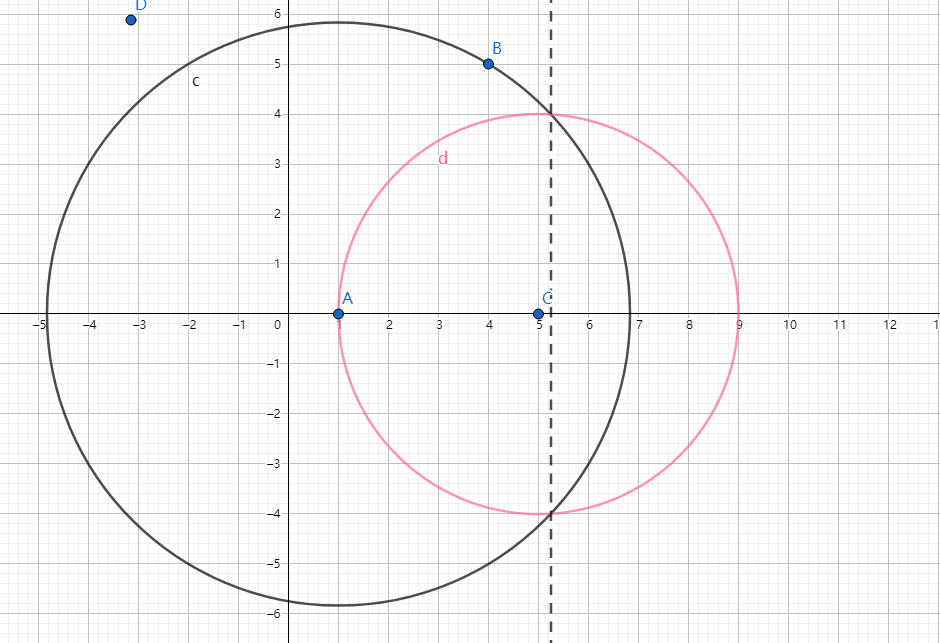
证明的话依然是利用解析式去证明,和上个性质证明过程没有太大区别。
性质5
两条直线或曲线的夹角大小在反演变换下是不变的。
体现了反演的反向保角性
性质6
两个圆相切,它们的反演图形也相切
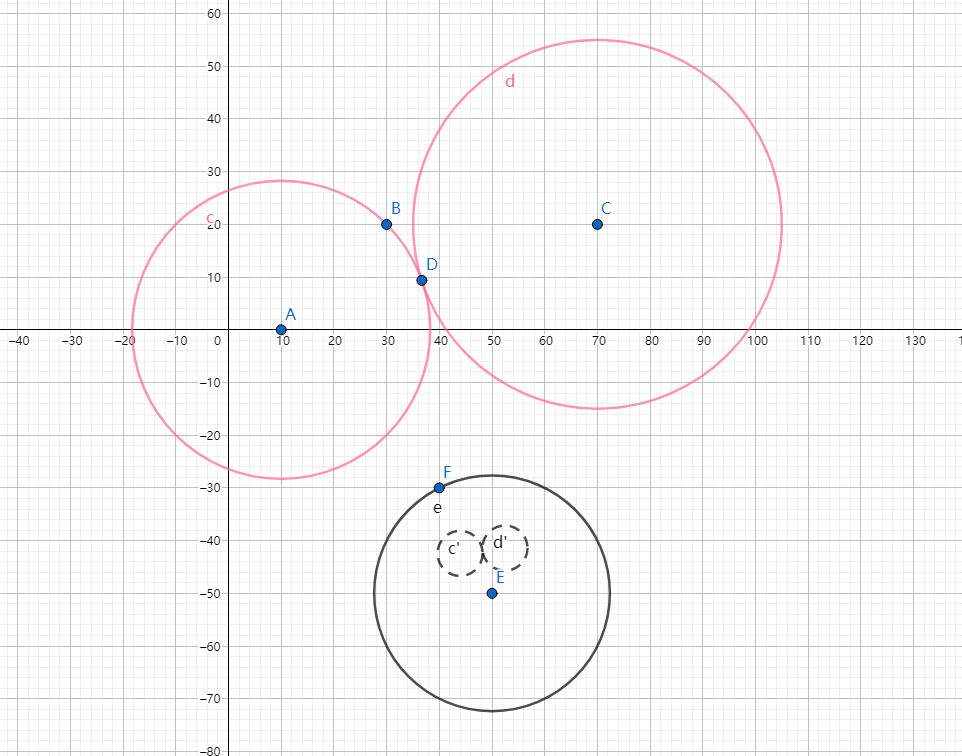
(易证)
后记
现在你可以去尝试暴切CMO了