计算几何大水题!!!
计算几何选做
还挺简单的一道题,不难看出答案是具有单调性的而且,求最大攻击力最小,很容易就会想到二分。
假设我们当前二分的值为mid,现在需要去解决的是如何去check当前的答案合不合法,其实就是解一个形如:
atki+dnfi+atkiab+dnfiba≤mid
的一个不等式,上述式子中说明了每个妖精的战斗力很显然是atki+dnfi+atkiab+dnfiba,现在我们可以对式子进行变形:
atki+dnfi+atkiab+dnfiba−mid≤0
设A=atki,B=atki+dnfi−mid,C=dnfi再将ab设为x,式子变为:
Ax+B+Cx1≤0
两边同时乘以x得:
Ax2+Bx+C≤0
check时判断范围二次函数解集是否有交即可,还有注意解是要大于0的。
时间复杂度O(nlogn)
先只考虑给定窗口的左上角哪些位置可以圈到一颗星星,不难发现下图:
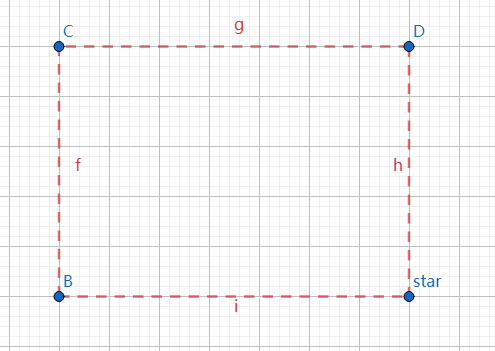
右下角为我们需要圈到的星星,整个虚线区域就是可以使我们所用的窗口的左上角满足条件的解集(不包括边界),将这个矩形的权值设为这颗星星的亮度,对于每一颗星星都有对应的一个这样的矩形,转化为重合的区域最大权值为多少,这样就可以用扫描线转化为区间最值问题。
处理边界的话可以将所有星星的坐标偏移0.5,就可以很好的处理边界问题。
题意很简单,求对平面上点的最小矩形覆盖。
不难想到,旋转卡壳可以轻松的解决这个问题,对于最小矩形覆盖,其最小矩形的一条边必定在这nn个点的凸包上,这样我们就先求出凸包再使用旋转卡壳,找到在以当前边为矩形的一条边时,在最左边,最右边,最上边的点,然后用向量加减的方法求出矩形的高和宽,再进一步求面积就好了。
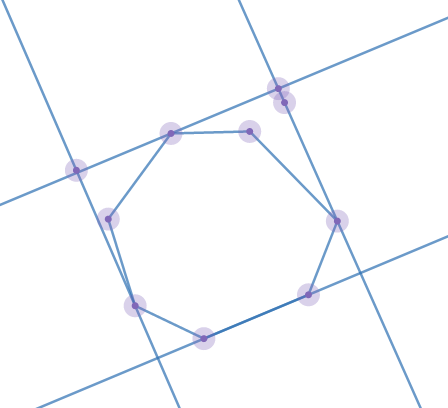
(注意是否有无解的情况)
然后还有一道类似的题目,就是数据不太一样。
无非就是向量的旋转和直线的求交点而已。
题意大概就是有m种操作:
- 插入一个点
- 询问Ax+By=C这条直线是否和当前插入的点组成的凸包有交
既然不强制在线,就可以离线下来利用CDQ分治的思想,去处理每个询问之前的修改操作对询问的影响,接下来就是考虑如何计算影响。
给出的限制条件其实就是判断当前已经插入的所有点,带入式子后是否同号,其实就是判断是否都在同一个半平面,进一步转化问题为,凸包的上下两个点的值的判断,可以看一个图(我搬的)
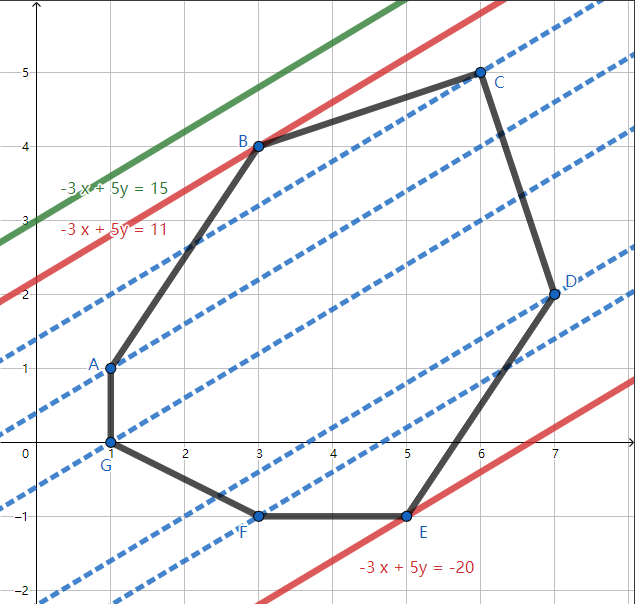
判断时,只需要计算Ax+By来作为值去判断,假设计算出来的最大值为Cmax最小值为Cmin,当Cmin<C<Cmax时很明显就是与凸包有交。
维护时需要维护一个上凸包和一个下凸包,利用凸包单调性,去旋转判断,记录每条直线的Cmin和Cmax最后统一判断即可。
时间复杂度O(nlogn)
题意就是求平面内矩形的周长并,可以看一下图
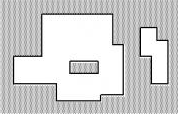
图很形象吧,很明显扫描线可以轻易的解决这道题,(但是数据范围太小,连n2都能暴碾过去,而且似乎跑的比扫描线还快)。
首先和求面积并一样的方法去维护,同时数据规模也不需要我们去离散化,现在考虑如何去统计答案,
每次加入一条线段时,对整棵线段树,中维护的区间覆盖的个数的改变其实就是我们需要累加的答案,很容易想到不是吗?
但是一次扫描还不够,要扫两次,先扫一遍x轴再扫一遍y轴即可,不过也可以在扫x个轴的时候同时计算y轴的答案,扫一遍也能解决问题,就是需要注意一些小细节。
首先需要注意,权值线段树的值域为[−1e5,1e5],然后非常重要的一点就是,在线段树上一段区间的长度为r−l+1,但在计算边长的时候对于坐标系中的一条线段,其长为r−l,也就是说我们在修改线段时需要对右端点-1,接下来还有一个比较重要的点,那就是,在排序时如果两个线段在同一直线上需要让执行加入线段操作的在前,比如:
1
2
3
4
5
6
| input:
2
0 0 4 4
0 4 4 8
output:
24
|
这组数据,对应过来就是
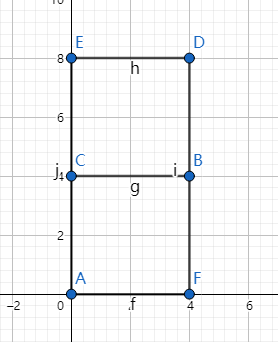
如过我们在计算x轴时先删去了BC再执行插入就会算了两遍贡献,y轴上也同理,排序的时候需要注意一下。
很清晰的题意对吧,首先我们先考虑没有树木阻挡的情况,求最小时间,一种做法就是二分加网络流,二分枚举最小时间,然后建图的话就是对于每个巫妖向它能以攻击到的精灵连一条权值为1的边,然后从源点向每个巫妖连一条权值为在限制的时间内能以攻击的最多次数的边,每个精灵向汇点连一条权值为1的边,最后跑最大流即可。
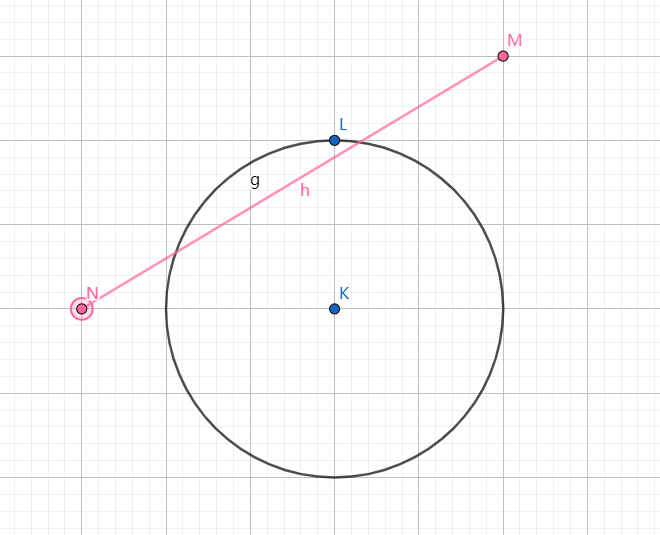
现在加入树木,树木能以影响两个点的话就是判断,圆与线段是否有交点,如下:
-
线段的两个端点都在圆内,无交点。
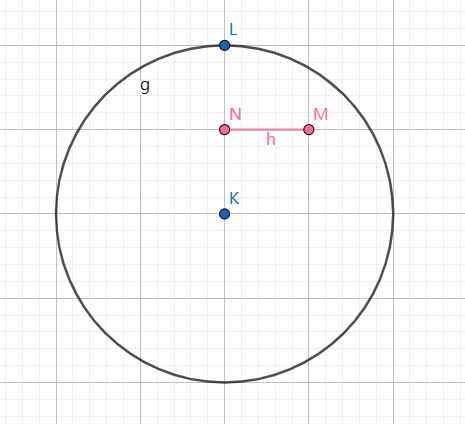
-
线段的两个端点一个在园内一个在圆外,有交点。
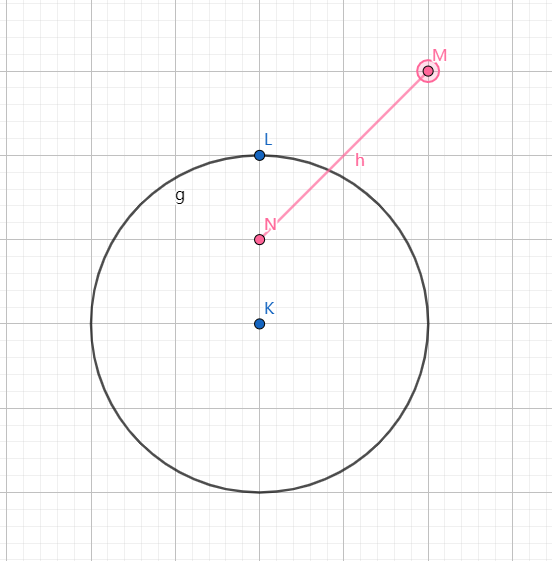
-
线段的两个端点均在圆外,判断方法就是从圆心向线段所在的直线作垂线,长度记为d如果d>r则无交点,如果d≤r需要去判断圆心与端点的连线与线段所成的角是否为锐角。
(说实话,这题数据挺水的),首先n3枚举处理出每个巫妖所能打到的精灵,然后二分跑网络流即可。
给一个比较清晰的图吧。
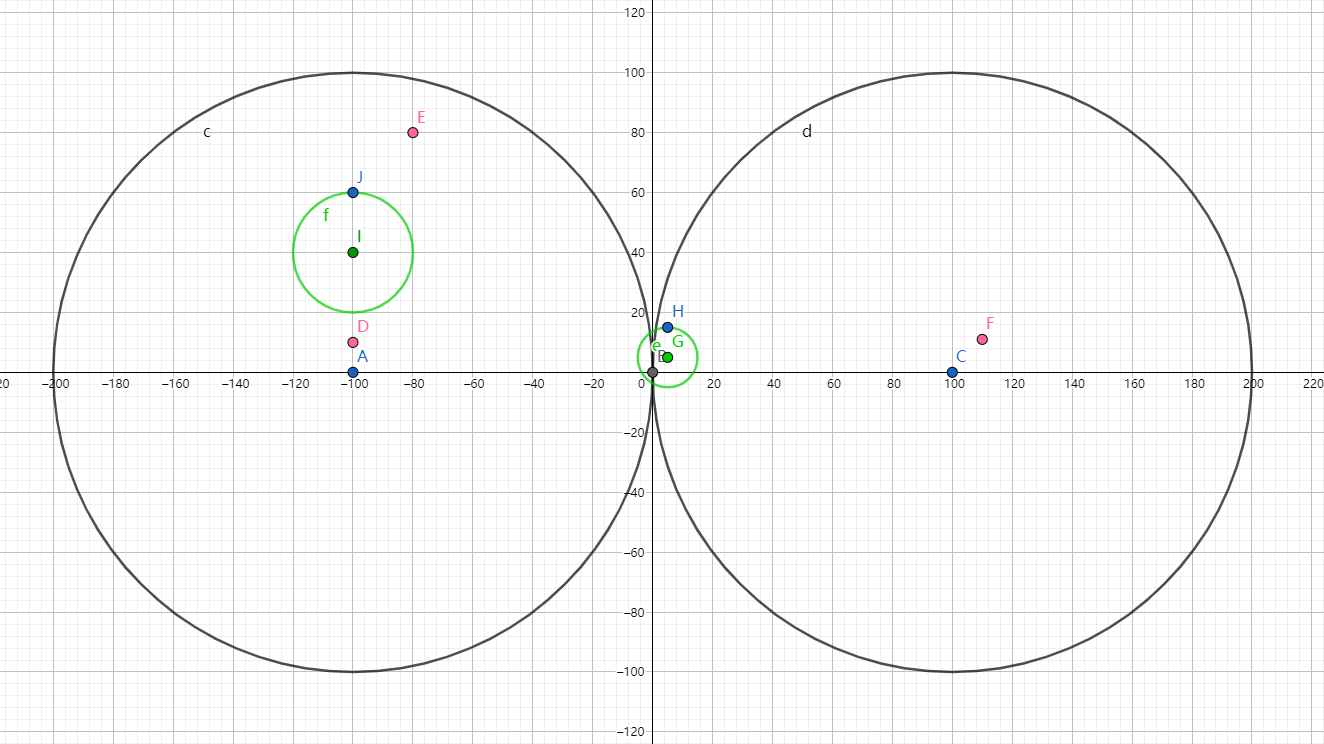
题意就是求圆的异或并,看到n≤2×105,肯定是不能乱搞过去的,但是注意到题目中的已知这些圆两两没有交点,即两圆的关系只存在相离和包含,就会不难得出一个性质:如果将每个圆按x坐标排序后,假设有一条垂直于x轴的扫描线,从左往右扫,一个圆肯定是比它包含的圆先出现,后消失的。
显然扫描线可以解决这个问题,现在需要知道如何去判断奇偶性,每次扫描线向右移动的时候,我们肯定不能插入一个圆,来计算与扫描线的交点,但是我们用set维护,分别插入一个圆的上圆弧和下圆弧,按与扫描线的交点排序来判断以下情况:
-
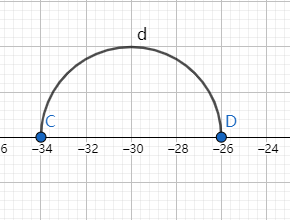
插入的圆弧是set中的唯一一段圆弧,为奇面积。
-
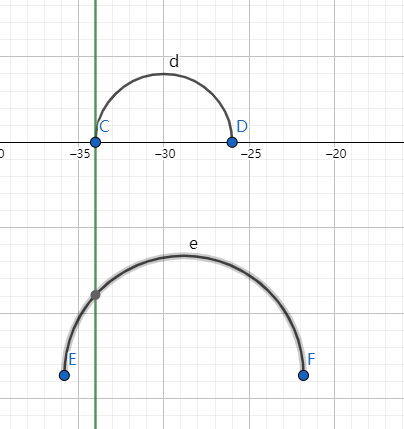
插入圆弧的前驱为上圆弧,该圆的奇偶性与其相同(因为扫描线从左到右移动时,由于圆两两之间没有交点,前驱为上圆弧时肯定不包含该圆)
-
插入圆弧的前驱为下圆弧时,该圆的奇偶性与其相反(该圆被前驱的圆包含)
最后ans加上奇面积减去偶面积就可以了
需要注意的几个点:
- set重载小于号时要重载成严格小于,set具有不可重性,只需要计算与扫描线交点时加上一个eps就行了
- 统计答案时开long long
根据题意列出式子,设三段距离分别为x,y,z对于第i个人和第j个人,i可以得到冠军,当且仅当:
vi,1x+vi,2y+vi,3z<vj,1x+vj,2y+vj,3z
发现有三个未知数,但因为总路程是一样的可以假设总路程为“1”,这样就有:
vi,1x+vi,2y+vi,31−x−y<vj,1x+vj,2y+vj,31−x−y
考虑化成Ax+By+C>0的形式:
vj,1x+vj,2y+vj,31−x−y−vi,1x−vi,2y−vi,31−x−y>0
进一步整理得:
(vj,11−vi,11+vi,31−vj,31)x+(vj,21−vi,21+vi,31−vj,31)y+vj,31−vi,31>0
其中A=vj,11−vi,11+vi,31−vj,31,B=vj,21−vi,21+vi,31−vj,31,C=vj,31−vi,31,半平面交求解即可,时间复杂度O(n2)。
需要注意计算系数时,分式的分子为1很明显会产生较大的误差, 可以在式子两边同时乘以一个较大的数,来解决这个问题,更需要说明的是根据我们设的x,y很明显x+y≤1,需要对其进行限制。
关于半平面交
解决这类问题很明显是半平面交的很大用处,来判断多元一次不等式组是否有解,在推理完式子后,往往需要插入直线,选择直线上的一个点和方向向量,一般建议化简式子为Ax+By+C≥0的形式(或不带等),取直线的“左侧”,这里的左侧是依照选取的方向向量来说的,对于选取方向向量,我们需要让其满足式子中的条件,又需要让其满足求左侧的交,是不能随便选直线上的两个点来确定的,其实多画图就不难发现方向向量取(B,−A)是可以满足要求的,起点的话,一般选x=0处的取值,但是有时需要考虑值域。在求交的时候,需要额外注意题目中的值域条件,在求交的集合中加入对应的直线。
首先假设P点为(x,y),那么根据题意就有:
(x0−x,y0−y)×(x1−x,y1−y)<(xi−1−x,yi−1−y)×(xi−x,yi−y)
进一步化简得:
(x0−x)(y1−y)−(x1−x)(y0−y)<(xi−1−x)(yi−y)−(xi−x)(yi−1−y)
拆开式子,
x0y1−x0y−xy1+xy−x1y0+x1y+xy0−xy<xi−1yi−xi−1y−xyi+xy−xiyi−1+xiy+xyi−1−xy
转化为Ax+By+C>0的形式,
(−yi+yi−1+y1−y0)x+(−xi−1+xi+x0−x1)y+xi−1yi−xiyi−1−x0y1+x1y0>0
其中A=−yi+yi−1+y1−y0,B=−xi−1+xi+x0−x1,C=xi−1yi−xiyi−1−x0y1+x1y0,半平面交求解即可,别忘了把解限制在凸多边形内。
其实看到题目就可以发现,最终向量之和最大其实是闵可夫斯基和上离原点最远的点,对于多个凸包的闵可夫斯基和,可以用启发式合并,每次合并小的, 复杂度O(nlogn)。












