Link Cut Tree

  学习笔记13 分钟读完 (大约1982个字)0次访问

初探Link Cut Tree

Link Cut Tree

概念

Link Cut Tree 简称LCT，属于实链剖分，是应用比较广泛的链剖分之一， 链剖分其实就是对树的一些边进行轻重划分的操作，在实现树上的修改和查询时能以以一个较为优秀的复杂度去解决问题，主要还是有三类：重链剖分， 实链剖分， 和长链剖分。

性质

首先虚实剖和轻重剖最大的不同还是LCT可以做到动态的连边断边，用起来比较灵活，可以解决一些树剖解决不了的问题，主要用splay来维护，LCT支持的操作主要有：

  • 查询、修改链上的信息
  • 随意指定原树的根
  • 动态连边，删边
  • 合并两个树
  • 动态维护连通性

使用LCT 解决问题时需要不断维护以下性质：

  1. 每一个splay维护的时一条从上到下按在原树中深度严格递增的路径，splay的中序遍历就可以得到对应的路径，也就是说不能把深度相同的放在一个splay中，也就是说一个splay维护的是对应到原树上的一条链。
  2. 每个节点只能包含在一个splay中。
  3. 边分为实边和虚边，实边包含在splay中， 虚边总是由一棵splay指向另一个节点（该splay中维护的链深度小的链的一端的父亲节点）。
  4. 当某点有多个儿子时只能向其中一个儿子拉一条实链，其他的儿子连成虚链，由对应儿子所属的splay的根节点的父亲指向该点，并且从该点不能访问其的虚儿子， 但从其虚儿子可以访问到该点也就是“认父不认子”。

支持的操作实现

access

LCT的核心操作，是其他操作的基础。

首先根据性质3， 两个点不一定是直接联通的（不在一个splay中，也就是说路径上不全是实边，有虚边）,access操作就可以打通两个点之间的路径，将其变成实边。

假设现在我们有这样的一棵树，

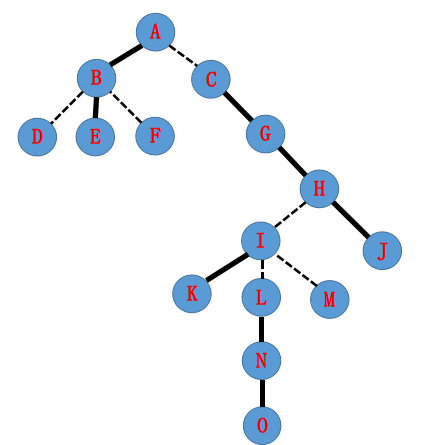
1309909-20180123095924037-1618037447 1.png

所构成的LCT可能长这个样子，

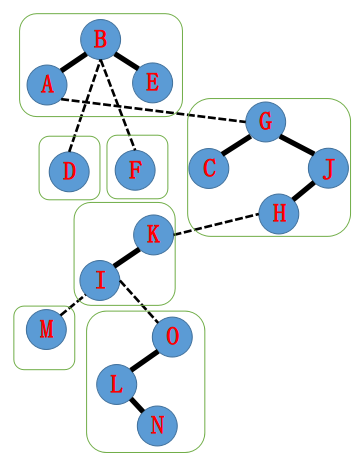
1309909-20180123095955350-1680422636.png

假设我们要将A−NA - N的路径打通，首先splay(N)， 将其变为所在splay的根节点， 然后把OO变为虚儿子，

然后接着处理II，将II的右儿子设为NN ,

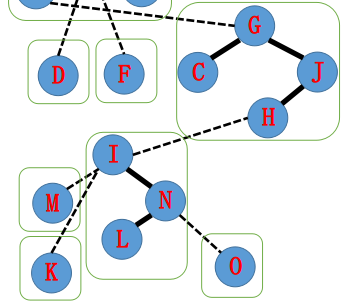
1309909-20180123110156272-1242463729.png

接着splay(H),

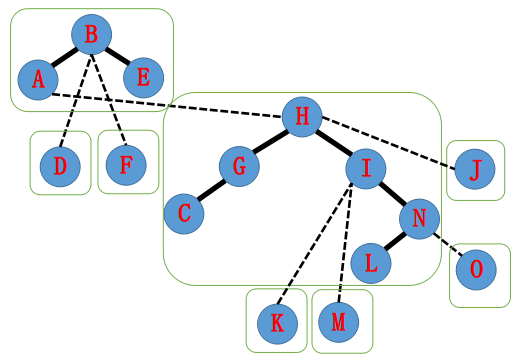
1309909-20180123110209772-2057141058.png

HH 指向AA ，splay(A)，

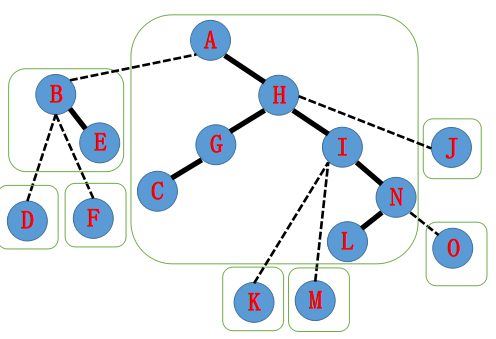
1309909-20180123110213709-49169640.png

然后就完成了。

其实就是先转到根，然后换儿子，更新信息， 当前操作点切换为轻边所指的父亲。

1
2
3
4
5
void access(int x) // root -> x
{
    for(int y = 0; x; y = x, x = fa(y))
    	splay(x), rs(x) = y, push_up(x); // 旋转到根， 换儿子， 更新信息
}

makeroot

上面的access操作只是求出了根到某个点的路径，更多时候，我们需要获取指定两个节点的路径，但有可能这两个点之间的路径不是严格递增的，这样的话根据我们维护的性质，这两个点是不会出现在同一个splay中的， 这时我们可以将指定点称为原树的根，来实现makeroot， 首先access(x)后， xx一定时splay中，中序遍历最后的点，也就是深度最大的点，接着splay(x)，xx将没有右子树，然后反转整个splay， xx就成为了深度最小的点，也就是根节点。

1
2
3
4
5
6
7
8
9
10
11
12
void recover(int x) // 区间反转
{
    swap(ls(x), rs(x));
    t[x].rev ^= 1; // 区间反转标记
}

void makeroot(int x) // 换根
{
    access(x);
    splay(x);
    recover(x);
}

findroot

寻找x,yx, y 在原树中的根节点，来判断连通性。

1
2
3
4
5
6
7
8
9
10
11
12
int findroot(int x) // 找根
{
    access(x);
    splay(x);
    while(ls(x)) // 找深度小的链的一端
    {
        push_down(x);
        x = ls(x);
    }
    splay(x);
    return x;
}

split

spilt操作是用来拉出x→yx \rightarrow y的路径，变成一个splay。

1
2
3
4
5
6
void split(int x, int y) // x -> y
{
    makeroot(x);
    access(y);
    splay(y);
}

link操作用来连边。

1
2
3
4
5
6
void link(int x, int y) // link x -> y
{
    makeroot(x);
    if(findroot(y) != x) // 判断是否在同一棵树中
        fa(x) = y;
}

cut

cut操作用来断边。

1
2
3
4
5
6
7
8
9
void cut(int x, int y) // cut x -> y
{
    makeroot(x);
    if(findroot(y) == x && fa(y) == x && !ls(y)) // 判断操作是否合法
    {
        fa(y) = rs(x) = 0;
        push_up(x);
	}
}

splay 的一些操作

大部分差不多。

首先核心的rotate操作

1
2
3
4
5
6
7
8
9
10
11
12
13
void rotate(int x)
{
    int y = fa(x), z = fa(y);
    bool res = check(x);
    if(nroot(y)) t[z].son[check(y)] = x; // 不同之处，需要判断是不是为根， 如果连的是轻边 它的父亲儿子是不能有它的，不是根再更新儿子。
    fa(x) = z;
    t[y].son[res] = t[x].son[res ^ 1];
    fa(t[x].son[res ^ 1]) = y;
    t[x].son[res ^ 1] = y;
    fa(y) = x;
    push_up(y);
    push_up(x);
}

然后是splay，

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
void splay(int x)
{
    int y = x, z, top = 0;
    int st[N]; st[++top] = y;
    while(nroot(y)) st[++top] = y = fa(y); // 记录到根的路径
    while(top) push_down(st[top--]); // 下穿标记
    while(nroot(x))
    {
        int y = fa(x), z = fa(y);
        if(nroot(y))
     		(check(y) ^ check(y)) ? rotate(x) : rotate(y);
       rotate(x);
    }
    push_up(x);
}

更新信息的操作，根据题意更改，这里以P3690 【模板】动态树（Link Cut Tree）为例，

1
2
3
4
5
6
7
8
9
10
11
12
void push_up(int x)
{
    t[x].sum = t[ls(x)].sum ^ t[rs(x)].sum ^ t[x].val;
}

void push_down(int x)
{
    if(!t[x].rev) return;
    if(ls(x)) recover(ls(x));
    if(rs(x)) recover(rs(x));
    t[x].rev = 0;
}

check和nroot，

1
2
bool check(int x) {return rs(fa(x)) == x;}
bool nroot(int x) {return ls(fa(x)) == x || rs(fa(x)) == x;} // 不是根为true

附上一个完整代码P3690 【模板】动态树（Link Cut Tree）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
#include<bits/stdc++.h>
using namespace std;

const int N = 1e5 + 10;
const int M = 3e5 + 10;

int n, m;

int a[N];

namespace LCT
{
    struct splaytree
    {
        int son[2], val, father, sum;
        int rev;
        #define ls(p) t[p].son[0]
        #define rs(p) t[p].son[1]
        #define fa(p) t[p].father
    }t[N << 1];

    bool check(int x) {return rs(fa(x)) == x;}

    bool nroot(int x) {return ls(fa(x)) == x || rs(fa(x)) == x;}

    void push_up(int x)
    {
        t[x].sum = t[ls(x)].sum ^ t[rs(x)].sum ^ t[x].val;
    }

    void recover(int x)
    {
        swap(ls(x), rs(x));
        t[x].rev ^= 1;
    }

    void push_down(int x)
    {
        if(!t[x].rev) return;
        if(ls(x)) recover(ls(x));
        if(rs(x)) recover(rs(x));
        t[x].rev = 0;
    }

    void rotate(int x)
    {
        int y = fa(x), z = fa(y);
        bool res = check(x);
        if(nroot(y)) t[z].son[check(y)] = x;
        fa(x) = z;
        t[y].son[res] = t[x].son[res ^ 1];
        fa(t[x].son[res ^ 1]) = y;
        t[x].son[res ^ 1] = y;
        fa(y) = x;
        push_up(y);
        push_up(x);
    }

    int st[N];
    
    void splay(int x)
    {
        int y = x, z, top = 0;
        st[++top] = y;
        while(nroot(y)) st[++top] = y = fa(y);
        while(top) push_down(st[top--]);
        while(nroot(x))
        {
            y = fa(x), z = fa(y);
            if(nroot(y))
                (check(x) ^ check(y)) ? rotate(x) : rotate(y);
            rotate(x);
        }
        push_up(x);
    }

    void access(int x)
    {
        for(int y = 0; x; y = x, x = fa(y))
            splay(x), rs(x) = y, push_up(x);
    }

    void makeroot(int x)
    {
        access(x);
        splay(x);
        recover(x);
    }

    int findroot(int x)
    {
        access(x);
        splay(x);
        while(ls(x))
        {
            push_down(x);
            x = ls(x);
        }
        splay(x);
        return x;
    }

    void split(int x, int y)
    {
        makeroot(x);
        access(y);
        splay(y);
    }

    void link(int x, int y)
    {
        makeroot(x);
        if(findroot(y) != x)
            fa(x) = y;
    }

    void cut(int x, int y)
    {
        makeroot(x);
        if(findroot(y) == x && fa(y) == x)
        {
            fa(y) = rs(x) = 0;
            push_up(x);
        }
    }
}

int main()
{
	scanf("%d%d", &n, &m);
	for(int i = 1; i <= n; i++)
		scanf("%d", &a[i]);
    for(int i = 1; i <= n; i++)
        LCT::t[i].val = a[i];
	for(int i = 1; i <= m; i++)
	{
		int opt, x, y;
		scanf("%d%d%d", &opt, &x, &y);
		if(opt == 0)
		{
            LCT::split(x, y);
            printf("%d\n", LCT::t[y].sum);
		}
		if(opt == 1)
		{
            LCT::link(x, y);
		}
		if(opt == 2)
		{
            LCT::cut(x, y);
		}
		if(opt == 3)
		{
            LCT::splay(x);
            LCT::t[x].val = y;
        }
    }
	return 0;
}

参考文献

[1] LCT总结——概念篇Flash_Hu

Link Cut Tree

https://jekyll-y.github.io/2022/09/14/Link-Cut-Tree/

作者

Jekyll_Y

发布于

2022-09-14

更新于

2023-03-02

许可协议

#

评论

Follow

目录

×