矩阵树定理讲解
对于一个n × n n \times n n × n
det ( A ) = ∑ P ( − 1 ) μ ( P ) ∏ i = 1 n A ( i , p i ) \det(A) = \sum_{P}(-1)^{\mu(P)}\prod_{i = 1} ^ n A(i, p_i)
det ( A ) = P ∑ ( − 1 ) μ ( P ) i = 1 ∏ n A ( i , p i )
其中P P P 1 − n 1 - n 1 − n μ ( P ) \mu(P) μ ( P ) P P P
单位矩阵I I I 1 1 1
交换矩阵的两行,行列式变号(改变了奇数个逆序对)。
若某一行乘以k k k k k k
行的线性性。
∣ a + a ′ b + b ′ c d ∣ = ∣ a b c d ∣ + ∣ a ′ b ′ c d ∣ \begin{vmatrix} a + a'& b+ b' \\ c & d\end{vmatrix}
= \begin{vmatrix} a & b \\ c & d\end{vmatrix} +
\begin{vmatrix} a'& b' \\ c & d\end{vmatrix}
∣ ∣ ∣ ∣ ∣ a + a ′ c b + b ′ d ∣ ∣ ∣ ∣ ∣ = ∣ ∣ ∣ ∣ ∣ a c b d ∣ ∣ ∣ ∣ ∣ + ∣ ∣ ∣ ∣ ∣ a ′ c b ′ d ∣ ∣ ∣ ∣ ∣
有某两行一样的矩阵,行列式为0 0 0
粗略的证明:根据1,假设我们交换相同的两行,会使行列式变号, 但是交换后,行列式并没有发生改变,也就是行列式只能等于0 0 0
用矩阵的上一行加上另一行的倍数, 行列式不变。
证明:
∵ ∣ a b c ⋯ a b c ∣ = 0 = ∣ a b c ⋯ k a k b k c ∣ = 0 ∴ ∣ a b c ⋯ d + k a e + k b f + k c ∣ = ∣ a b c ⋯ k a k b k c ∣ + ∣ a b c ⋯ d e f ∣ = ∣ a b c ⋯ d e f ∣ \because \begin{vmatrix} a & b & c \\ & \cdots \\ a & b & c\end{vmatrix} = 0
=\begin{vmatrix} a & b & c \\ & \cdots \\ ka & kb & kc\end{vmatrix} = 0 \\
\therefore \begin{vmatrix} a & b & c \\ & \cdots \\ d + ka & e + kb &f + kc\end{vmatrix}
= \begin{vmatrix} a & b & c \\ & \cdots \\ ka & kb & kc\end{vmatrix} + \begin{vmatrix} a & b & c \\ & \cdots \\ d & e & f\end{vmatrix} = \begin{vmatrix} a & b & c \\ & \cdots \\ d & e & f\end{vmatrix}
∵ ∣ ∣ ∣ ∣ ∣ ∣ ∣ a a b ⋯ b c c ∣ ∣ ∣ ∣ ∣ ∣ ∣ = 0 = ∣ ∣ ∣ ∣ ∣ ∣ ∣ a k a b ⋯ k b c k c ∣ ∣ ∣ ∣ ∣ ∣ ∣ = 0 ∴ ∣ ∣ ∣ ∣ ∣ ∣ ∣ a d + k a b ⋯ e + k b c f + k c ∣ ∣ ∣ ∣ ∣ ∣ ∣ = ∣ ∣ ∣ ∣ ∣ ∣ ∣ a k a b ⋯ k b c k c ∣ ∣ ∣ ∣ ∣ ∣ ∣ + ∣ ∣ ∣ ∣ ∣ ∣ ∣ a d b ⋯ e c f ∣ ∣ ∣ ∣ ∣ ∣ ∣ = ∣ ∣ ∣ ∣ ∣ ∣ ∣ a d b ⋯ e c f ∣ ∣ ∣ ∣ ∣ ∣ ∣
首先高斯消元的过程中我们用到的是交换两行,行列式的值变号, 某一行乘上一个数,行列式乘上对应值,一行加上另一行的倍数,行列式不变,最后得到上三角矩阵后,把影响逆回去即可。
P7112 行列式求值
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 #include <bits/stdc++.h> using namespace std;#define int long long const int N = 610 ;int a[N][N];int n, p;signed main () scanf ("%lld%lld" , &n, &p); for (int i = 1 ; i <= n; i++) for (int j = 1 ; j <= n; j++) scanf ("%lld" , &a[i][j]); int ans = 1 , f = 1 ; for (int i = 1 ; i <= n; i++) { for (int j = i + 1 ; j <= n; j++) { while (a[i][i]) { int div = a[j][i] / a[i][i]; for (int k = i; k <= n; k++) a[j][k] = (a[j][k] - div * a[i][k] % p + p) % p; swap (a[i], a[j]); f = - f; } swap (a[i], a[j]); f = -f; } } for (int i = 1 ; i <= n; i++) ans = (ans * a[i][i]) % p; ans = f * ans; printf ("%lld" , (ans + p) % p); return 0 ; }
矩阵树定理(Matrix-tree Theorem) 是把图的生成树个数和矩阵行列式联系起来的定理。(有很大的用处!)
首先设有无向图G = ( V , E ) G = (V, E) G = ( V , E ) p p p q q q
然后我们把G G G G G G 关联矩阵(Incidence Matrix) M ( G ) M(G) M ( G ) p × q p \times q p × q
M i , j = { − 1 v i i s t h e s t a r t o f e j 1 v i i s t h e e n d o f e j 0 o r t h e r w i s e M_{i,j} =
\left\{
\begin{aligned}
& -1 & v_i \ is \ the \ start\ of \ e_j \\
& 1 & v_i \ is \ the \ end \ of \ e_j \\
& 0 & ortherwise
\end{aligned}
\right.
M i , j = ⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ − 1 1 0 v i i s t h e s t a r t o f e j v i i s t h e e n d o f e j o r t h e r w i s e
接着定义G G G 拉普拉斯矩阵(Laplacian Matrix) L ( G ) L(G) L ( G ) p × p p \times p p × p
L i , j = { − m i , j i ≠ j , m i , j e d g e b e t w e e n v i , v j d e g ( v i ) i = j L_{i, j} =
\left\{
\begin{aligned}
& -m_{i, j} &i \not = j \ ,m_{i,j} \ edge \ between \ v_i, v_j \\
& deg(v_i) &i = j
\end{aligned}
\right.
L i , j = { − m i , j d e g ( v i ) i = j , m i , j e d g e b e t w e e n v i , v j i = j
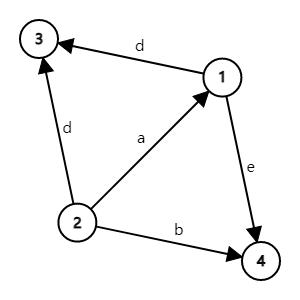
注意到M M M G G G L L L
对应的关联矩阵M M M
∣ 1 0 0 − 1 − 1 − 1 − 1 − 1 0 0 0 0 1 1 0 0 1 0 0 1 ∣ \begin{vmatrix}1&0&0&-1&-1\\-1&-1&-1&0&0\\0&0&1&1&0\\0&1&0&0&1\end{vmatrix}
∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ 1 − 1 0 0 0 − 1 0 1 0 − 1 1 0 − 1 0 1 0 − 1 0 0 1 ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣
对应的拉普拉斯矩阵L L L
∣ 3 − 1 − 1 − 1 − 1 3 − 1 − 1 − 1 − 1 2 0 − 1 − 1 0 2 ∣ \begin{vmatrix}
3 & -1 & -1 & -1 \\
-1 & 3 & -1 & -1\\
-1 & -1 & 2 & 0\\
-1 & -1 & 0 & 2
\end{vmatrix}
∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ 3 − 1 − 1 − 1 − 1 3 − 1 − 1 − 1 − 1 2 0 − 1 − 1 0 2 ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣
另外L L L − 1 -1 − 1 G G G
M M T = L M M ^T = L M M T = L M T M^T M T M M M
证明:由定义易得:( M M T ) i , j = ∑ e k ∈ E M i , k M k , j T = ∑ e k ∈ E M i , k M j , k (MM^T)_{i,j} = \sum_{e_k \in E} M_{i,k} M ^T_{k,j} = \sum_{e_k \in E} M_{i,k}M_{j,k} ( M M T ) i , j = ∑ e k ∈ E M i , k M k , j T = ∑ e k ∈ E M i , k M j , k i = j i = j i = j i ≠ j i \not = j i = j − m i , j -m_{i,j} − m i , j
接下来引入一些M M M Reduce Incidence Matrix ,M 0 M_0 M 0 M M M ( p − 1 ) × q (p - 1) \times q ( p − 1 ) × q
定义一个( p − 1 ) × ( p − 1 ) (p - 1) \times (p - 1) ( p − 1 ) × ( p − 1 ) M 0 [ S ] M_0[S] M 0 [ S ] S = { i 1 , i 2 , ⋯ , i p − 1 } ∈ { 1 , 2 , ⋯ , q } S = \{i _ 1, i_2, \cdots ,i_{p-1}\} \in \{1, 2, \cdots , q\} S = { i 1 , i 2 , ⋯ , i p − 1 } ∈ { 1 , 2 , ⋯ , q } M 0 M_0 M 0 p − 1 p - 1 p − 1
令S S S E E E p − 1 p - 1 p − 1 G ′ = ( V , S ) G' = (V,S) G ′ = ( V , S ) det M 0 [ S ] = 0 \det M_0[S] = 0 det M 0 [ S ] = 0 G ′ G' G ′ det M 0 [ S ] = ± 1 \det M_0[S] = \pm 1 det M 0 [ S ] = ± 1 det \det det
Binet-Cauchy Theorem 设A = ( a i , j ) A = (a_{i,j}) A = ( a i , j ) m × n m \times n m × n B = ( b i , j ) B = (b_{i,j}) B = ( b i , j ) n × m n \times m n × m det ( A B ) = ∑ S ( det A [ s ] ) ( det B [ s ] ) \det (AB) = \sum_{S} (\det A[s])(\det B[s]) det ( A B ) = ∑ S ( det A [ s ] ) ( det B [ s ] ) S S S m m m { 1 , 2 , ⋯ , n } \{ 1, 2, \cdots , n\} { 1 , 2 , ⋯ , n }
Matrix-tree Theorem 设图G = ( V , E ) G = (V, E) G = ( V , E ) L L L G G G det L 0 \det L_0 det L 0 L 0 L_0 L 0 L L L i i i i i i
设G G G n n n
D i , i ( G ) = d e g ( i ) , D i , j ( G ) = 0 , i ! = j D_{i,i}(G) = deg(i), \ D_{i, j}(G) = 0, \ i != j
D i , i ( G ) = d e g ( i ) , D i , j ( G ) = 0 , i ! = j
其邻接矩阵为
A i , j ( G ) = A j , i ( G ) = e ( i , j ) , i ≠ j A_{i, j}(G) = A_{j , i}(G) = e(i, j), i \not= j
A i , j ( G ) = A j , i ( G ) = e ( i , j ) , i = j
其拉普拉斯矩阵为
L ( G ) = D ( G ) − A ( G ) L(G) = D(G) - A(G)
L ( G ) = D ( G ) − A ( G )
设G G G n n n
D i i o u t ( G ) = d e g o u t ( i ) , D i j o u t = 0 , i ≠ j D^{out}_{ii}(G) = \mathrm{deg^{out}}(i), D^{out}_{ij} = 0, i\neq j
D i i o u t ( G ) = d e g o u t ( i ) , D i j o u t = 0 , i = j
类似的入度矩阵也这样定义
定义其邻接矩阵为
A i , j = e ( i , j ) , i ≠ j A_{i,j} = e(i, j), \ i \not = j
A i , j = e ( i , j ) , i = j
其拉普拉斯矩阵L o u t L^{out} L o u t
L o u t ( G ) = D o u t ( G ) − A ( G ) L^{out}(G) = D^{out}(G) - A(G)
L o u t ( G ) = D o u t ( G ) − A ( G )
L i n L^{in} L i n
L i n ( G ) = D i n ( G ) − A ( G ) L^{in}(G) = D^{in}(G) - A(G)
L i n ( G ) = D i n ( G ) − A ( G )
对于带权无向图,若存在边u → v u\rightarrow v u → v c c c D x , x + c , D y , y + c , A x , y + c , A y , x + c D_{x, x} + c, D_{y,y} + c, A_{x, y} + c, A_{y, x} + c D x , x + c , D y , y + c , A x , y + c , A y , x + c
对于带权有向图,若存在边u → v u \rightarrow v u → v c c c D y , y + c D_{y, y} + c D y , y + c D x , x + c D_{x, x} + c D x , x + c A x , y + c A_{x, y} + c A x , y + c
P6178Matrix-Tree 定理
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 #include <bits/stdc++.h> using namespace std;#define ll long long const int N = 310 ;const int mod = 1e9 + 7 ;ll D[N][N], A[N][N], L[N][N]; int n, m, t;void add (int u, int v, int c, int type) if (t == 0 ) { (D[u][u] += c) %= mod; (D[v][v] += c) %= mod; (A[u][v] += c) %= mod; (A[v][u] += c) %= mod; } else { (D[v][v] += c) %= mod; (A[u][v] += c) %= mod; } } ll ans; void gauss () ll f = 1 ; for (int i = 2 ; i <= n; i++) { for (int j = i + 1 ; j <= n; j++) { while (L[i][i]) { ll div = L[j][i] / L[i][i]; for (int k = i; k <= n; k++) L[j][k] = ((L[j][k] - L[i][k] * div % mod) % mod + mod) % mod; swap (L[i], L[j]); f = -f; } f = -f; swap (L[i], L[j]); } } ans = f; for (int i = 2 ; i <= n; i++) ans = (ans % mod * (L[i][i] + mod) % mod + mod) % mod; } int main () scanf ("%d%d%d" , &n, &m, &t); for (int i = 1 ; i <= m; i++) { int x, y, z; scanf ("%d%d%d" , &x, &y, &z); add (x, y, z, t); } for (int i = 1 ; i <= n; i++) for (int j = 1 ; j <= n; j++) L[i][j] = (D[i][j] - A[i][j] + mod) % mod; gauss (); printf ("%lld" , ans); return 0 ; }
上面的构造方式只是求了每个生成树边权乘积的和, 接下来需要解决,每个生成树边权之和的和,对于一条边权为w w w x x x w x + 1 wx + 1 w x + 1 ( a + b x ) ( c + d x ) = a c + ( a d + b c ) x (a + bx) (c + dx) = ac + (ad + bc)x ( a + b x ) ( c + d x ) = a c + ( a d + b c ) x a + b x c + d x = a c + b c − a d c 2 x \frac{a + bx} {c + dx} = \frac{a}{c} + \frac{bc - ad}{c ^ 2}x c + d x a + b x = c a + c 2 b c − a d x × \times × C + D x = 1 c + d x C + Dx = \frac{1}{c + dx} C + D x = c + d x 1 ( C + D x ) ( c + d x ) = 1 m o d x 2 (C + Dx)(c + dx) = 1 \bmod x^2 ( C + D x ) ( c + d x ) = 1 m o d x 2 C = 1 c , D = − d c 2 C = \frac{1}{c}, D = -\frac{d}{c^2} C = c 1 , D = − c 2 d a + b x a + bx a + b x a c + b c − a d c 2 x \frac{a}{c} + \frac{bc - ad}{c^2}x c a + c 2 b c − a d x
P6624 作业题
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 #include <bits/stdc++.h> using namespace std;#define ll long long const int N = 310 ;const int mod = 1e9 + 7 ;ll D[N][N], A[N][N], L[N][N]; int n, m, t;void add (int u, int v, int c, int type) if (t == 0 ) { (D[u][u] += c) %= mod; (D[v][v] += c) %= mod; (A[u][v] += c) %= mod; (A[v][u] += c) %= mod; } else { (D[v][v] += c) %= mod; (A[u][v] += c) %= mod; } } ll ans; void gauss () ll f = 1 ; for (int i = 2 ; i <= n; i++) { for (int j = i + 1 ; j <= n; j++) { while (L[i][i]) { ll div = L[j][i] / L[i][i]; for (int k = i; k <= n; k++) { L[j][k] = ((L[j][k] - L[i][k] * div % mod) % mod + mod) % mod; } swap (L[i], L[j]); f = -f; } f = -f; swap (L[i], L[j]); } } ans = f; for (int i = 2 ; i <= n; i++) ans = (ans % mod * (L[i][i] + mod) % mod + mod) % mod; } int main () scanf ("%d%d%d" , &n, &m, &t); for (int i = 1 ; i <= m; i++) { int x, y, z; scanf ("%d%d%d" , &x, &y, &z); add (x, y, z, t); } for (int i = 1 ; i <= n; i++) for (int j = 1 ; j <= n; j++) L[i][j] = (D[i][j] - A[i][j] + mod) % mod; gauss (); printf ("%lld" , ans); return 0 ; }
证明以后再补吧(逃