P3830 [SHOI2012]随机树

P3830 [SHOI2012]随机树

题解

题意

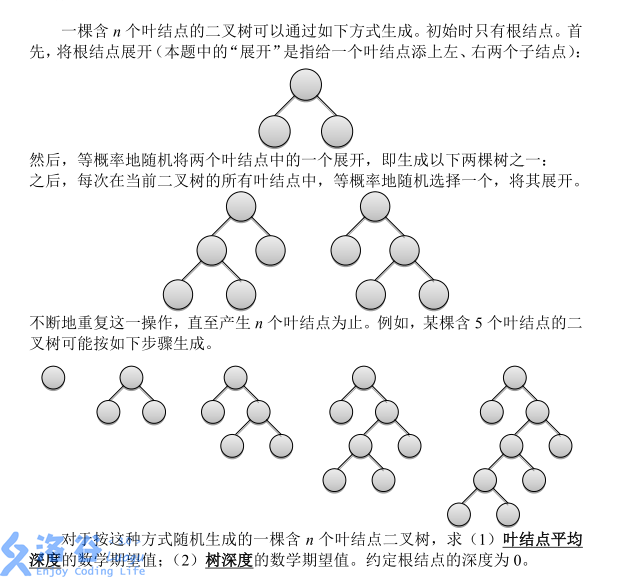
解法

首先解决第一个问题，叶节点平均深度的期望值，可以设$f_i$表示有$i$个叶子节点的随机树的平均深度的期望值，可以得到转移方程为

$$f_i = \frac{f_{i - 1} \times (i - 1) - f_{i - 1} + (f_{i - 1} + 1) \times 2}{i}$$

其实就是计算当前有$i$个叶子节点时在$i - 1$个叶子节点的情况下，展开一个节点，计算其深度的影响，化简后也就是

$$f_i= f_{i- 1} + \frac{2} {i}$$

然后第二个问题就麻烦了，树深度的期望值，首先根据期望的线性性有

$$E(x) = \sum_{i = 1} ^ {+ \infty} P(i \le x)$$

然后可以设$f_{i, j}$为有$i$个叶子节点且深度大于等于$j$的树的出现概率，得出转移方程为

$$f_{i, j} = \sum_{k = 1} ^ {i - 1} \frac{f_{k, j - 1} + f_{i - k, j - 1} - f_{k, j - 1} \times f_{i - k, j - 1}}{i- 1}$$

首先$k$时枚举的左子树中叶子节点的数量，然后求左子树中深度大于等于$j - 1$ 的概率，由于左右子树深度都大于$j - 1$的情况在$f_{k , j - 1}$和$f_ {i - k, j - 1}$中都统计过，所以要去减去重复的部分，对于除以$i - 1$的部分可以去看这个证明。

#include <bits/stdc++.h>

using namespace std;

const int N = 110;

int n, q;

namespace SubTask1
{
    double f[N];

    void getans()
    {
        for(int i = 2; i <= n; i++)
            f[i] = f[i - 1] + 2.0 / i;
        printf("%.6lf", f[n]);
    }
}

namespace SubTask2
{
    double f[N][N];

    void getans()
    {
        for(int i = 1; i <= n; i++)
            f[i][0] = 1;
        for(int i = 2; i <= n; i++)
        {
            for(int j = 1; j < i; j++)
            {
                for(int k = 1; k < i; k++)
                    f[i][j] += f[k][j - 1] + f[i - k][j - 1] - f[k][j - 1] * f[i - k][j - 1];
                f[i][j] /= (i - 1) * 1.0;
            }
        }
        double ans = 0;
        for(int i = 1; i < n; i++)
            ans += f[n][i];
        printf("%.6lf", ans);
    }
}

int main()
{
    scanf("%d%d", &q, &n);
    if(q == 1)SubTask1::getans();
    if(q == 2)SubTask2::getans();
    return 0;
}